filmov
tv
Can You Find The Area of Greatest Rectangle in a Ellipse | Maximum Area | Ellipse

Показать описание
Can You Find The Area of Greatest Rectangle in a Ellipse | Maximum Area | Ellipse
Topics Covered :-
maximum area, max area, maxima and minima, maximum area of rectangle, maximize area, maximum rectangle size, ellipse, ellipse class 11, ellipses, ellipse jee, how to draw ellipse, ellipse jee mains, ellipse iit jee, conic sections ellipse, ellipse jee main, ellipse one shot, ellipse equation, ellipse jee mains questions, equation of an ellipse, ellipse jee mains 2022, ellipse conic, ellipse 1 shot, ellipse iit jee questions, standard equation of ellipse, what is an ellipse
Math Booster will provide you quality content on different topics of mathematics such as algebra, calculus etc.. that will be helpful for math olympiad or any other competitive exams. In every video, you will get a new math problem with step by step solution. So Subscribe the channel and press the bell icon to get notified of my new videos.
Join this channel to get access to perks:
Watch More Videos
----------------------------------
For Math Olympiad
For IIT-JEE
Algebra
Geometry
Trigonometry
Quadratic Equations
logarithms
Sequence And Series
Functions
Differentiation
Integration
Number Theory
Permutation And Combination
Probability
Limits
Differential Equation
Interesting Math
#mathbooster #matholympiad #mathematics #premath #sybermath #blackpenredpen #justalgebra #math #maths #olympiadmathematics #matholympics #mindyourdecisions #solveforx #mathproblems #algebra
Topics Covered :-
maximum area, max area, maxima and minima, maximum area of rectangle, maximize area, maximum rectangle size, ellipse, ellipse class 11, ellipses, ellipse jee, how to draw ellipse, ellipse jee mains, ellipse iit jee, conic sections ellipse, ellipse jee main, ellipse one shot, ellipse equation, ellipse jee mains questions, equation of an ellipse, ellipse jee mains 2022, ellipse conic, ellipse 1 shot, ellipse iit jee questions, standard equation of ellipse, what is an ellipse
Math Booster will provide you quality content on different topics of mathematics such as algebra, calculus etc.. that will be helpful for math olympiad or any other competitive exams. In every video, you will get a new math problem with step by step solution. So Subscribe the channel and press the bell icon to get notified of my new videos.
Join this channel to get access to perks:
Watch More Videos
----------------------------------
For Math Olympiad
For IIT-JEE
Algebra
Geometry
Trigonometry
Quadratic Equations
logarithms
Sequence And Series
Functions
Differentiation
Integration
Number Theory
Permutation And Combination
Probability
Limits
Differential Equation
Interesting Math
#mathbooster #matholympiad #mathematics #premath #sybermath #blackpenredpen #justalgebra #math #maths #olympiadmathematics #matholympics #mindyourdecisions #solveforx #mathproblems #algebra
Комментарии
 0:04:33
0:04:33
 0:10:26
0:10:26
 0:07:14
0:07:14
 0:08:58
0:08:58
 0:11:38
0:11:38
 0:22:10
0:22:10
 0:02:48
0:02:48
 0:04:43
0:04:43
 0:14:43
0:14:43
 0:10:22
0:10:22
 0:02:41
0:02:41
 0:12:43
0:12:43
 0:01:39
0:01:39
 0:10:55
0:10:55
 0:09:58
0:09:58
 0:08:42
0:08:42
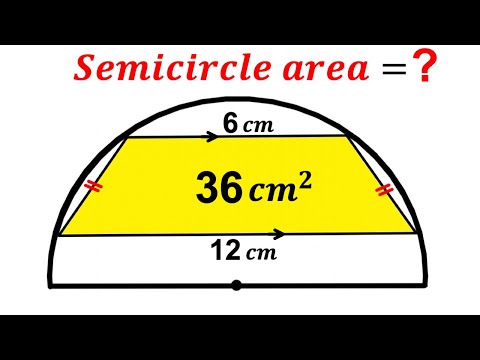 0:10:21
0:10:21
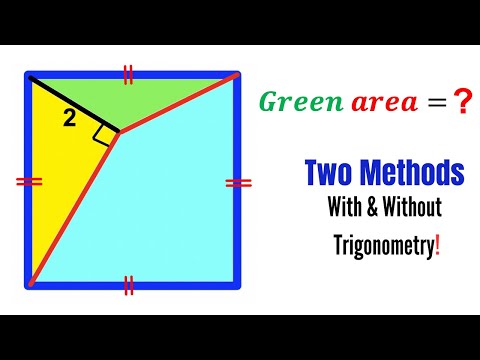 0:09:08
0:09:08
 0:03:59
0:03:59
 0:10:13
0:10:13
 0:09:04
0:09:04
 0:11:48
0:11:48
 0:08:44
0:08:44
 0:08:04
0:08:04