filmov
tv
Determine the intervals a function is increasing and decreasing and extrema using

Показать описание
👉 Learn how to find the extreme values of a function using the first derivative test. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A method that can be used to obtain the extreme values of a function is the first derivative test.
To obtain the extreme values of a function using the first derivative test, first, we obtain the first derivative of the function. Next, we set the first derivative equal to zero and solve for x. the values of x obtained are the critical points of the function. On a number line, we chose points to the left and to the right of the critical points found and substitute into the original function. The intervals where the result obtained by substituting the points into the original function is positive, then the function is increasing on those intervals while the intervals where the result obtained by substituting the points into the original function is negative, then the function is decreasing on those intervals.
Organized Videos:
✅Applications of the Derivative
✅Determine Increasing or Decreasing Function From a Table
✅Concavity of Functions
✅Extreme Value Theorem of Functions
✅First Derivative Test for Functions
✅Find the Critical Values of a Function
✅Extrema, Concavity, Increasing Decreasing Intervals from a Graph
✅Sketch the Graph of the First and Second Derivative
✅Find the Points of Inflection of a Function
✅Second Derivative Test For a Function
✅Intermediate Value Theorem of Functions
Connect with me:
#derivatives #brianmclogan
To obtain the extreme values of a function using the first derivative test, first, we obtain the first derivative of the function. Next, we set the first derivative equal to zero and solve for x. the values of x obtained are the critical points of the function. On a number line, we chose points to the left and to the right of the critical points found and substitute into the original function. The intervals where the result obtained by substituting the points into the original function is positive, then the function is increasing on those intervals while the intervals where the result obtained by substituting the points into the original function is negative, then the function is decreasing on those intervals.
Organized Videos:
✅Applications of the Derivative
✅Determine Increasing or Decreasing Function From a Table
✅Concavity of Functions
✅Extreme Value Theorem of Functions
✅First Derivative Test for Functions
✅Find the Critical Values of a Function
✅Extrema, Concavity, Increasing Decreasing Intervals from a Graph
✅Sketch the Graph of the First and Second Derivative
✅Find the Points of Inflection of a Function
✅Second Derivative Test For a Function
✅Intermediate Value Theorem of Functions
Connect with me:
#derivatives #brianmclogan
 0:02:56
0:02:56
 0:11:08
0:11:08
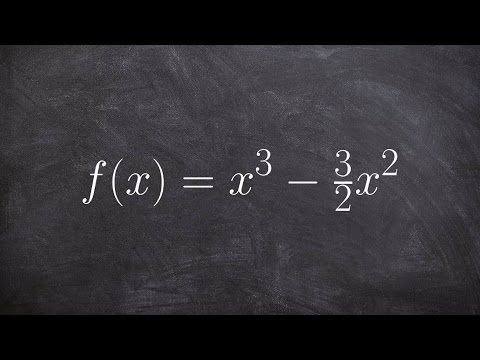 0:05:36
0:05:36
 0:08:26
0:08:26
 0:06:24
0:06:24
 0:05:55
0:05:55
 0:10:42
0:10:42
 0:03:56
0:03:56
 0:10:05
0:10:05
 0:00:38
0:00:38
 0:04:32
0:04:32
 0:01:16
0:01:16
 0:04:13
0:04:13
 0:10:51
0:10:51
 0:06:51
0:06:51
 0:06:47
0:06:47
 0:03:50
0:03:50
 0:02:36
0:02:36
 0:01:50
0:01:50
 0:02:33
0:02:33
 0:04:16
0:04:16
 0:04:35
0:04:35
 0:05:51
0:05:51
 0:11:45
0:11:45