filmov
tv
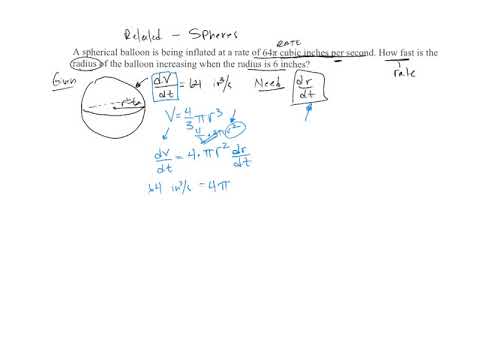
Related Rates (Lecture Part 6) Rate of change of radius of sphere

Показать описание
In this related rates example, an excerpt of a Calculus 1 lecture, we discuss how to find the rate of change of a radius of a sphere when the radius is a particular size. The rate of change of the volume is constant.
Related Rates (Lecture Part 6) Rate of change of radius of sphere
Related Rates; Pencast 6
Parametric Equations and Calculus Part 6 Related Rates
Related rates (Lecture Part 5) Conical Tank Calculation
Related Rates Part 6 cars or trainsl
Implicit differentiation, what's going on here? | Chapter 6, Essence of calculus
Related Rates - Boat w/ Trig
Related Rates and Two Approaching Cars
[UCLA Math 31A] Follow along - practice final 1.3
Section 4.2, part 6: Yet Another Related Rates Example
Related Rates (Lecture Part 1) What are they?
Related rates (Lecture Part 2) Point Moving Along Curve, y = cos x
Related rates: balloon | Applications of derivatives | AP Calculus AB | Khan Academy
The Volume of a Cone Problem - Related Rates
3.1 Part 6/6: Rate of Change of Sales Application Problem | Applied Calculus
AP Calculus Related Rates - Spherical Problems
related rates
The Derivative (Part 6: The Chain Rule)
Lecture 6 - Growth (Alex Schultz)
Derivative Application: Related Rates | Calc 1 Simplified | Wizeprep
Related rates implicit differentiation find rate at which radius is changing with respect to time
REVISION SEMINAR: Maths 1M: Related rates, parametric curves, complex roots (Sem 1 2019)
Calculus Related Rate problem - Change of the volume of a sphere
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Комментарии
 0:03:51
0:03:51
 0:23:57
0:23:57
 0:33:19
0:33:19
 0:01:50
0:01:50
 0:04:21
0:04:21
 0:15:34
0:15:34
 0:15:11
0:15:11
 0:10:13
0:10:13
![[UCLA Math 31A]](https://i.ytimg.com/vi/9VXE3ORPqAk/hqdefault.jpg) 0:38:21
0:38:21
 0:31:11
0:31:11
 0:05:15
0:05:15
 0:03:43
0:03:43
 0:08:17
0:08:17
 0:08:42
0:08:42
 0:04:42
0:04:42
 0:04:02
0:04:02
 0:06:01
0:06:01
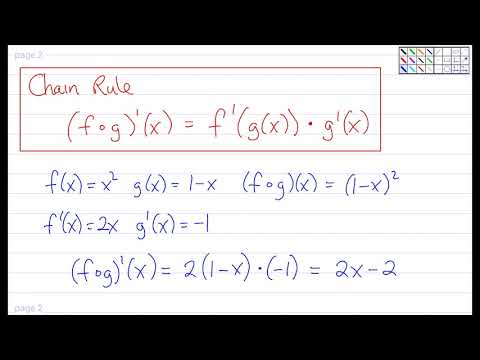 0:11:15
0:11:15
 0:47:28
0:47:28
 0:04:39
0:04:39
 0:01:53
0:01:53
 2:12:06
2:12:06
 0:02:18
0:02:18
 0:00:12
0:00:12