filmov
tv
Second Order Linear NonHomogeneous D.E. | Undetermined Coefficients | Linear Combination of G(x): 1

Показать описание
The 6 Rules-of-Thumb of the Method of Undetermined Coefficients
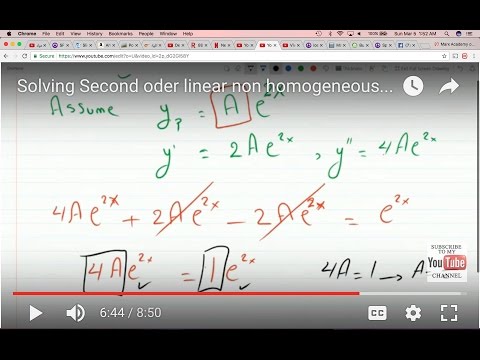
1. If an exponential function appears in g(x), the starting choice for Yₚ is an
exponential function of the same exponent.
2. If a polynomial appears in g(x), the starting choice for Yₚ is a generic
polynomial of the same degree.
3. If either cosine or sine appears in g(x), the starting choice for Yₚ needs to
contain both cosine and sine of the same frequency.
4. If g(x) is a sum of several functions, g(x) = g₁(x) + g₂(x) + … + gₙ(x),
separate it into n parts and solve them individually.
5. If g(x) is a product of basic functions, the starting choice for Yₚ(x) is chosen
based on:
i. Y(x) is a product of the corresponding choices of all the parts of g(x).
ii. There are as many coefficients as the number of distinct terms in Yₚ(x).
iii. Each distinct term must have its own coefficient, not shared with any
other term.
6. Before finalizing the choice of Yₚ(x), compare it against yₕ(x). If there is
any shared term between the two, the present choice of Yₚ(x) needs to be
multiplied by x. Repeat until there is no shared term.
Remember that, in order to use Rule 6 you always need to find the homogeneous solution first
1. If an exponential function appears in g(x), the starting choice for Yₚ is an
exponential function of the same exponent.
2. If a polynomial appears in g(x), the starting choice for Yₚ is a generic
polynomial of the same degree.
3. If either cosine or sine appears in g(x), the starting choice for Yₚ needs to
contain both cosine and sine of the same frequency.
4. If g(x) is a sum of several functions, g(x) = g₁(x) + g₂(x) + … + gₙ(x),
separate it into n parts and solve them individually.
5. If g(x) is a product of basic functions, the starting choice for Yₚ(x) is chosen
based on:
i. Y(x) is a product of the corresponding choices of all the parts of g(x).
ii. There are as many coefficients as the number of distinct terms in Yₚ(x).
iii. Each distinct term must have its own coefficient, not shared with any
other term.
6. Before finalizing the choice of Yₚ(x), compare it against yₕ(x). If there is
any shared term between the two, the present choice of Yₚ(x) needs to be
multiplied by x. Repeat until there is no shared term.
Remember that, in order to use Rule 6 you always need to find the homogeneous solution first
Комментарии
 0:41:28
0:41:28
 0:12:44
0:12:44
 0:26:58
0:26:58
 0:25:17
0:25:17
 0:03:55
0:03:55
 0:13:30
0:13:30
 0:15:25
0:15:25
 0:06:50
0:06:50
 0:16:45
0:16:45
 0:10:29
0:10:29
 0:09:34
0:09:34
 0:11:36
0:11:36
 0:16:42
0:16:42
 0:21:51
0:21:51
 0:24:17
0:24:17
 0:08:51
0:08:51
 0:06:41
0:06:41
 0:07:33
0:07:33
 0:12:21
0:12:21
 0:06:01
0:06:01
 0:04:35
0:04:35
 0:21:16
0:21:16
 0:01:47
0:01:47
 0:15:26
0:15:26