filmov
tv
Number Theory | Fermat's Little Theorem Example 1
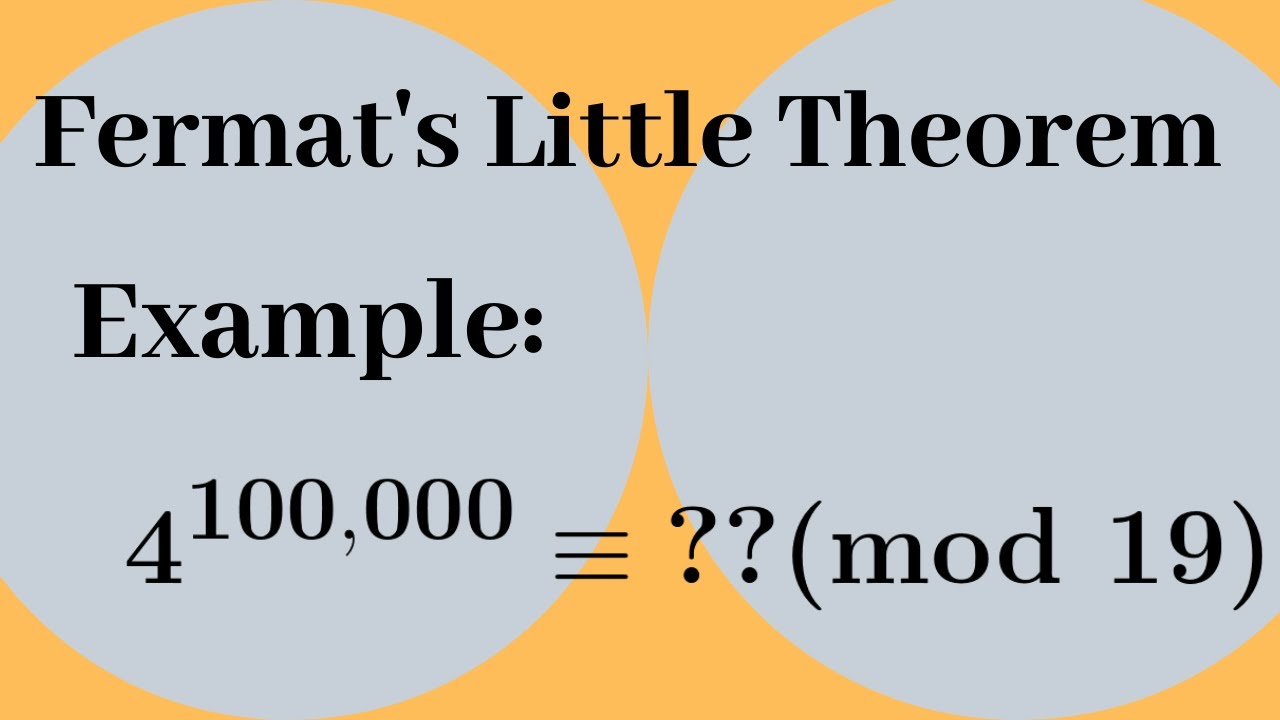
Показать описание
We give a few examples of applications of Fermat's Little Theorem.
Fermat's Little Theorem ← Number Theory
Fermat's Little Theorem
Number Theory | Fermat's Little Theorem
Number Theory: Fermat's Little Theorem
Fermat's Little Theorem - Explained in 5 minutes!
Applying Fermat's Little Theorem
Number Theory | Fermat's Little Theorem Example 1
Fermat's little theorem | Journey into cryptography | Computer Science | Khan Academy
LET Reviewer 2024 | Number Theory | Session 3
Fermat's Little Theorem
Proving Fermat' s Last Theorem (almost) in just 2 minutes !
Fermat's Little Theorem examples
Number Theory 10 29 Proof of Fermats Little Theorem
Solving Fermat's Little Theorem The Easy Way.😀
Number Theory | Corollaries to Fermat's Little Theorem
[Number Theory] Fermat's Little Theorem in English
LSU Number Theory Lecture 16 Fermats little theorem
Number Theory #5: Fermat's Little Theorem
Fermat's Little Theorem | A Proof of Fermat's Little Theorem from Number Theory
Number Theory | Fermat's Little Theorem
Fermat's Theorem Numerical examples | Important for exams
Euler's Totient Theorem and Fermat's Little Theorem - Complete Proof & Intuition
PotW: Solving a Linear Congruence using Fermat's Little Theorem [Number Theory]
Congruences | Part 9| Fermat's Theorem
Комментарии
 0:10:35
0:10:35
 0:07:31
0:07:31
 0:06:14
0:06:14
 0:08:07
0:08:07
 0:05:18
0:05:18
 0:02:16
0:02:16
 0:05:14
0:05:14
 0:06:06
0:06:06
 1:08:06
1:08:06
 0:19:16
0:19:16
 0:02:00
0:02:00
 0:11:45
0:11:45
 0:20:30
0:20:30
 0:08:42
0:08:42
 0:08:32
0:08:32
![[Number Theory] Fermat's](https://i.ytimg.com/vi/zgTUDCd8RRY/hqdefault.jpg) 0:11:44
0:11:44
 0:47:01
0:47:01
 0:06:11
0:06:11
 0:11:03
0:11:03
 0:05:08
0:05:08
 0:03:46
0:03:46
 0:15:29
0:15:29
 0:06:49
0:06:49
 0:12:50
0:12:50