filmov
tv
Similarity of Matrices

Показать описание
In linear algebra, two square matrices A and B are said to be similar if there exists an invertible matrix P such that P^-1AP = B.
Geometrically, similarity of matrices corresponds to a change of basis, where the matrix A is represented with respect to a new basis defined by the columns of P. The matrix B represents the same linear transformation as A, but with respect to the new basis.
Similarity of matrices has several important properties and applications in linear algebra, including:
Invariance of properties: Similar matrices have many properties that are invariant under similarity transformations, such as determinant, trace, rank, eigenvalues, and eigenvectors. In other words, if A and B are similar, then they have the same determinant, trace, rank, and characteristic polynomial, and they share the same eigenvalues and eigenvectors.
Diagonalization: If a matrix A is similar to a diagonal matrix D, then A is diagonalizable, meaning that it can be decomposed into a diagonal matrix with the eigenvalues of A along the diagonal and a matrix whose columns are the corresponding eigenvectors. This is because diagonal matrices are the simplest form of matrices and are easy to work with.
Applications: Similarity of matrices has many applications in various fields, such as control theory, image processing, and quantum mechanics. For example, it is used in control theory to transform the state-space representation of a system into a more convenient form, in image processing to perform transformations on images, and in quantum mechanics to relate the properties of different states of a quantum system.
It is worth noting that similarity is an equivalence relation on the set of square matrices, which means that it is reflexive, symmetric, and transitive. This implies that every matrix is similar to itself, and that if A is similar to B and B is similar to C, then A is similar to C.
#linearalgebra
#similarityofmatrices
Geometrically, similarity of matrices corresponds to a change of basis, where the matrix A is represented with respect to a new basis defined by the columns of P. The matrix B represents the same linear transformation as A, but with respect to the new basis.
Similarity of matrices has several important properties and applications in linear algebra, including:
Invariance of properties: Similar matrices have many properties that are invariant under similarity transformations, such as determinant, trace, rank, eigenvalues, and eigenvectors. In other words, if A and B are similar, then they have the same determinant, trace, rank, and characteristic polynomial, and they share the same eigenvalues and eigenvectors.
Diagonalization: If a matrix A is similar to a diagonal matrix D, then A is diagonalizable, meaning that it can be decomposed into a diagonal matrix with the eigenvalues of A along the diagonal and a matrix whose columns are the corresponding eigenvectors. This is because diagonal matrices are the simplest form of matrices and are easy to work with.
Applications: Similarity of matrices has many applications in various fields, such as control theory, image processing, and quantum mechanics. For example, it is used in control theory to transform the state-space representation of a system into a more convenient form, in image processing to perform transformations on images, and in quantum mechanics to relate the properties of different states of a quantum system.
It is worth noting that similarity is an equivalence relation on the set of square matrices, which means that it is reflexive, symmetric, and transitive. This implies that every matrix is similar to itself, and that if A is similar to B and B is similar to C, then A is similar to C.
#linearalgebra
#similarityofmatrices
 0:14:51
0:14:51
 0:08:13
0:08:13
 0:05:34
0:05:34
 0:08:47
0:08:47
 0:08:48
0:08:48
 0:01:28
0:01:28
 0:12:56
0:12:56
 0:17:01
0:17:01
 0:07:39
0:07:39
 0:23:23
0:23:23
 0:09:59
0:09:59
 0:35:04
0:35:04
 0:06:59
0:06:59
 0:19:08
0:19:08
 0:19:39
0:19:39
 0:04:50
0:04:50
 0:07:13
0:07:13
 0:06:00
0:06:00
 0:09:35
0:09:35
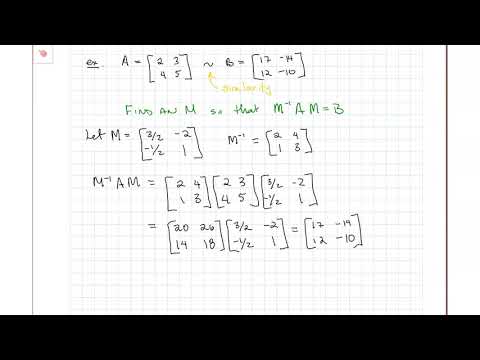 0:05:34
0:05:34
 0:12:41
0:12:41
 0:00:16
0:00:16
 0:08:43
0:08:43
 0:10:51
0:10:51