filmov
tv
Similar Matrices

Показать описание
MIT 18.06SC Linear Algebra, Fall 2011
Instructor: Ben Harris
A teaching assistant works through a problem on similar matrices.
License: Creative Commons BY-NC-SA
Instructor: Ben Harris
A teaching assistant works through a problem on similar matrices.
License: Creative Commons BY-NC-SA
Similar Matrices
Similar Matrices
Similar Matrices
Similar matrices have similar properties
Similar Matrices and Similarity Invariants | Linear Algebra
Similar matrices have the same characteristic polynomial
9 Similar matrices
Linear Algebra 5.2.2 Similar Matrices
Maths 2 | TA Session - Week 7a
5. Similar Matrices
Similar Matrices
Matrix similarity - example
Eigen values of Similar Matrices |Theorem for Similar matrix Transformation| Example
Similar Matrices, Change of Basis Matrices, and Diagonalisable Matrices (Linear Algebra)
Similar Matrices Transformation with Example || Linear Algebra Lecture Notes
2. Similar matrix definition | important results on Similar matrix | Linear algebra | AdnanAlig
The Similarity Relationship Represents a Change of Basis
Using similar matrices to find the matrix of a linear transformation, example 2
How similar matrix can be find out for a given matrix
Similar Matrices, Properties & Proofs
Diagonalization
Similar Matrices
Similar Matrices
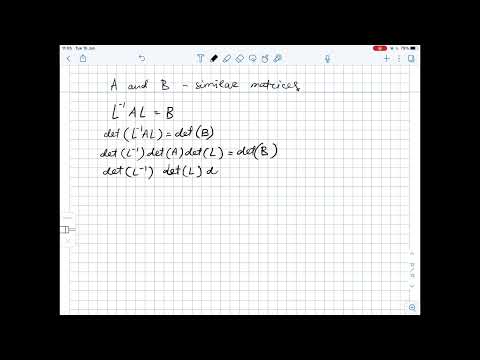
True or False - Determinants of two similar matrices are the same. Explain. | Plainmath
Комментарии
 0:14:51
0:14:51
 0:08:13
0:08:13
 0:06:59
0:06:59
 0:08:47
0:08:47
 0:12:56
0:12:56
 0:08:48
0:08:48
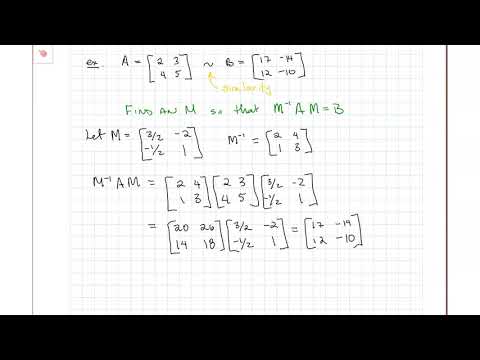 0:05:34
0:05:34
 0:06:06
0:06:06
 3:59:26
3:59:26
 0:23:23
0:23:23
 0:07:56
0:07:56
 0:05:34
0:05:34
 0:10:21
0:10:21
 0:03:44
0:03:44
 0:13:05
0:13:05
 0:04:49
0:04:49
 0:09:59
0:09:59
 0:04:11
0:04:11
 0:27:34
0:27:34
 0:05:29
0:05:29
 0:08:43
0:08:43
 0:07:56
0:07:56
 0:11:18
0:11:18
 0:02:39
0:02:39