filmov
tv
Similar Matrices

Показать описание
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015
Instructor: Gilbert Strang
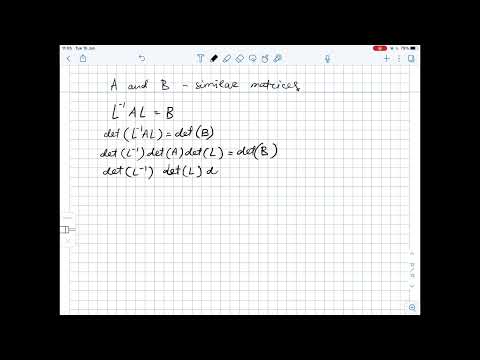
If A and B are "similar" then B has the same eigenvalues as A.
License: Creative Commons BY-NC-SA
Instructor: Gilbert Strang
If A and B are "similar" then B has the same eigenvalues as A.
License: Creative Commons BY-NC-SA
Similar Matrices
Similar Matrices
Similar matrices have similar properties
Similar matrices have the same characteristic polynomial
Similar Matrices and Similarity Invariants | Linear Algebra
Similar Matrices
Linear Algebra 5.2.2 Similar Matrices
9 Similar matrices
Matrix similarity - example
Similar Matrices
The Similarity Relationship Represents a Change of Basis
5. Similar Matrices
Similar Matrices, Change of Basis Matrices, and Diagonalisable Matrices (Linear Algebra)
Eigen values of Similar Matrices |Theorem for Similar matrix Transformation| Example
Similar Matrices Concept and its Properties - Know if Two matrices are Similar or not ?
Similar Matrices Transformation with Example || Linear Algebra Lecture Notes
Similar and Equivalent Matrices| Got explained Geometrically...!
True or False - Determinants of two similar matrices are the same. Explain. | Plainmath
Linear Algebra Sec. 6.4: Similar Matrices
Similar Matrices #maths #theorem #competitiveexam #tricks #shortcutmaths
Similar Matrix & Example Theorem: Relation of similarity is an equivalence relation
Similarity
Diagonalization
Similar Matrices, Properties & Proofs
Комментарии
 0:14:51
0:14:51
 0:08:13
0:08:13
 0:08:47
0:08:47
 0:08:48
0:08:48
 0:12:56
0:12:56
 0:06:59
0:06:59
 0:06:06
0:06:06
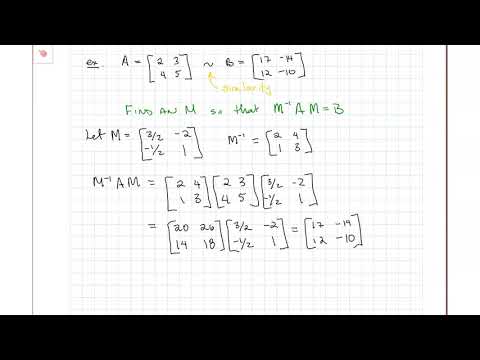 0:05:34
0:05:34
 0:05:34
0:05:34
 0:07:56
0:07:56
 0:09:59
0:09:59
 0:23:23
0:23:23
 0:03:44
0:03:44
 0:10:21
0:10:21
 0:09:35
0:09:35
 0:13:05
0:13:05
 0:06:00
0:06:00
 0:02:39
0:02:39
 0:14:09
0:14:09
 0:00:27
0:00:27
 0:07:13
0:07:13
 0:05:16
0:05:16
 0:08:43
0:08:43
 0:05:29
0:05:29