filmov
tv
What are derivatives in 3D? Intro to Partial Derivatives
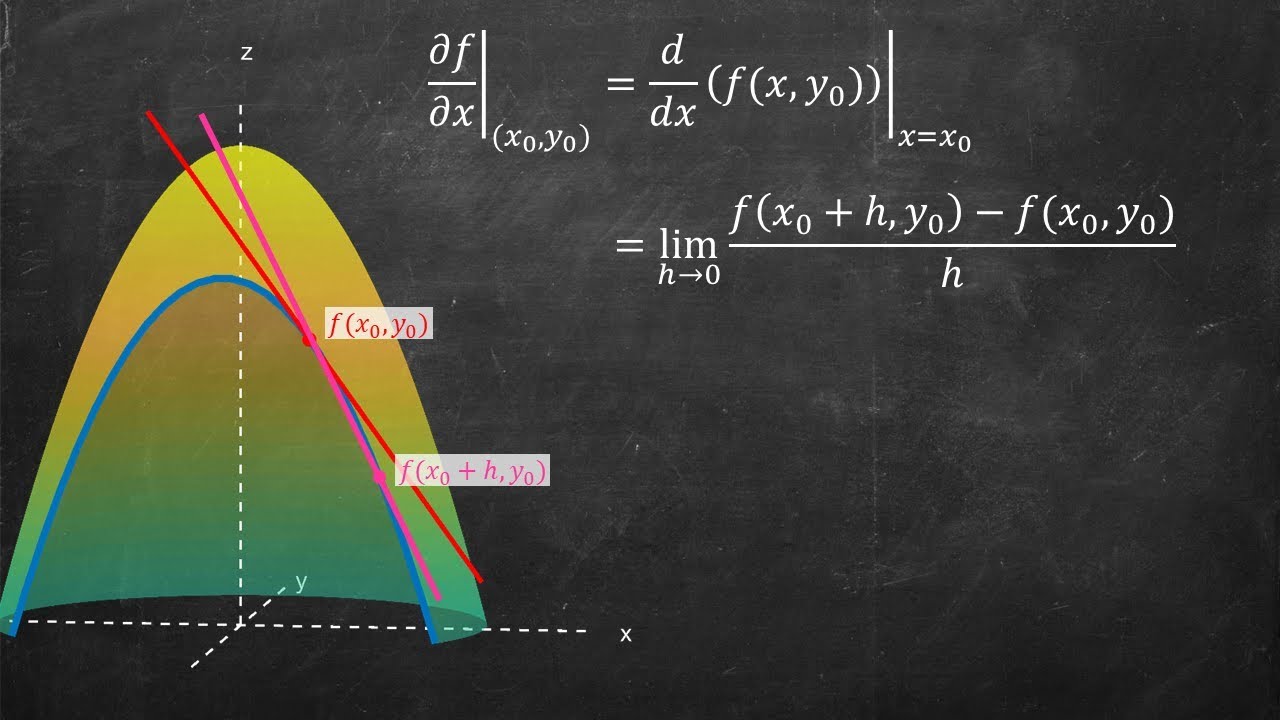
Показать описание
Imagine walking in only the x or only the y direction on a multivariable function f(x,y). The slope in these directions gives the idea of a partial derivative. It's much like the slope of a single variable function is the derivative, it is just now we have more than one direction we can go to. When heading, say, parallel to the x axis this is equivalent to saying the y is constant. This makes computing partial derivatives easy: just take a normal derivative as if the other variable is contant.
Sorry for the bad audio quality on this one!
****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************
****************************************************
Other Course Playlists:
***************************************************
► Want to learn math effectively? Check out my "Learning Math" Series:
►Want some cool math? Check out my "Cool Math" Series:
*****************************************************
*****************************************************
*****************************************************
This video was created by Dr. Trefor Bazett
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Sorry for the bad audio quality on this one!
****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************
****************************************************
Other Course Playlists:
***************************************************
► Want to learn math effectively? Check out my "Learning Math" Series:
►Want some cool math? Check out my "Cool Math" Series:
*****************************************************
*****************************************************
*****************************************************
This video was created by Dr. Trefor Bazett
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Комментарии
 0:08:53
0:08:53
 0:08:23
0:08:23
 0:05:24
0:05:24
 0:01:44
0:01:44
 0:07:15
0:07:15
 0:04:17
0:04:17
 0:04:23
0:04:23
 0:16:50
0:16:50
 0:00:55
0:00:55
 0:07:16
0:07:16
 0:17:05
0:17:05
 0:05:39
0:05:39
 0:03:01
0:03:01
 0:12:01
0:12:01
 0:17:34
0:17:34
 0:17:39
0:17:39
 0:05:15
0:05:15
 0:02:21
0:02:21
 0:12:39
0:12:39
 0:14:51
0:14:51
 0:18:36
0:18:36
 0:10:57
0:10:57
 0:05:21
0:05:21
 0:14:54
0:14:54