What the Quantum is a Path Integral?

Показать описание

With some help from Bart Simpson, we get introduced to one of the most fundamental problem solving tools in the physicist's toolbox. I hope you like being in every possible state at once!

Script:

We left off pondering the following question: How can we determine the probability that a quantum system in some initial state, I, will transition into some final state, F? It turns out, the answer to this question is surprisingly straightforward, at least conceptually.
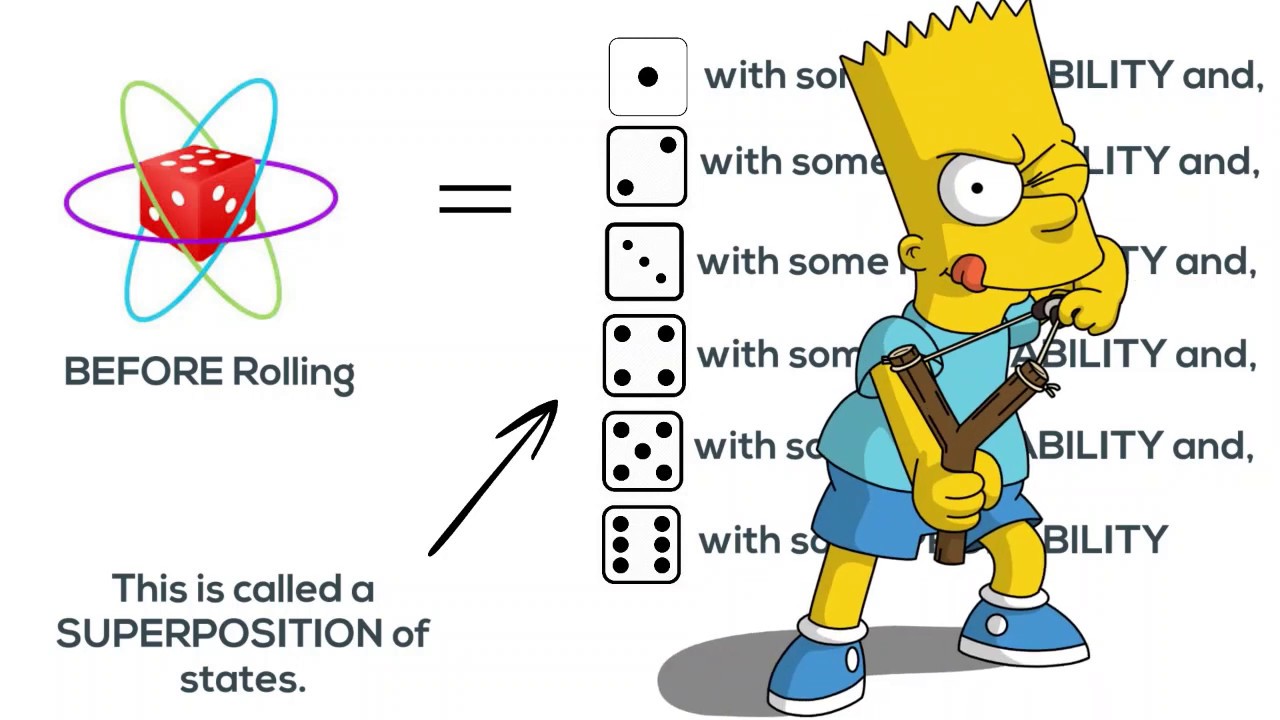
Because a quantum system cannot be in a determined state before it is measured, we are forced to say that the system is in a superposition of all its possible states at any given time. To understand what this means, think of a badly-behaved child sent to his room to go to sleep. He is so unpredictable, that once his door is closed you couldn’t say with any certainty where he’s going to be – in principle he could be anywhere in the room (except, perhaps, in his bed!). It is only when you open the door again and check on him that his state of being becomes clear.
Since a quantum system occupies all its possible states between measurements, it stands to reason that the probability the system will transition from one state of being to another state of being should be something like a sum over all the different ways this state transition could be achieved. For instance, the probability our child is on top of his dresser is something like the probability he jumped to it from his bed, plus the probability he climbed the drawers like a ladder, plus the probability he knocked it down to be able to sit atop it and so on over all of the different possible ways he could think to get up there.
In fact, this is exactly the recipe a Physicist follows to answer our question, only, because Physicists like to be fancy, we give the “sum over all the different ways” the complicated sounding name: Path Integral. At its core, the Path Integral formulation of Quantum Mechanics is really no more complicated than the sum we did in trying to predict where our child would be.