filmov
tv
Find positive integers x and y such that x^2-2^y=2021.

Показать описание
The video illustrates step-by-step how to find positive integers x and y such that x^2-2^y=2021.
Subscribe at:
#MathsEnhancer #MathematicalCompetition #MathematicalOlympiad #ChallengingMathematicsProblems #MathematicsCompetition #EnhanceMathematicsProblemSolvingSkills #Mathematics
#ImproveMathematicsGrades
Solve Diophantine equations
Solving Diophantine equations
Find integer solutions of exponential equations
AwesomeMath
Math Olympiad challenge
Challenging mathematics problems
Enhance mathematics problem solving skills
Mathematical competition questions
Mathematics competition questions
Improve mathematics grades
Olympics math
Olympics maths
Olympics mathematics
Olympics math competition
Math Olympiad training
International Mathematical Olympiad questions and solutions
International Mathematical Olympiad questions and answers
How to solve Olympiad question
How to solve International Mathematical Olympiad question
How to solve Olympiad Mathematics Question
How to prepare for Maths Olympiad
How to prepare for Math Olympiad
Olympiad mathematics competition
Olympiad exam
Olympiad exam sample paper
Maths Olympiad sample question
Maths Olympiad sample answer
Math Olympiad
Subscribe at:
#MathsEnhancer #MathematicalCompetition #MathematicalOlympiad #ChallengingMathematicsProblems #MathematicsCompetition #EnhanceMathematicsProblemSolvingSkills #Mathematics
#ImproveMathematicsGrades
Solve Diophantine equations
Solving Diophantine equations
Find integer solutions of exponential equations
AwesomeMath
Math Olympiad challenge
Challenging mathematics problems
Enhance mathematics problem solving skills
Mathematical competition questions
Mathematics competition questions
Improve mathematics grades
Olympics math
Olympics maths
Olympics mathematics
Olympics math competition
Math Olympiad training
International Mathematical Olympiad questions and solutions
International Mathematical Olympiad questions and answers
How to solve Olympiad question
How to solve International Mathematical Olympiad question
How to solve Olympiad Mathematics Question
How to prepare for Maths Olympiad
How to prepare for Math Olympiad
Olympiad mathematics competition
Olympiad exam
Olympiad exam sample paper
Maths Olympiad sample question
Maths Olympiad sample answer
Math Olympiad
Find Positive Integers x and y | U.K Maths Olympiad 2011
Find positive integers x, y, satisfying x^2+y^2=6625. Mathematics competition | Mathematics Olympiad
Find a pair of distinct positive integers x and y, which satisfy a quartic equation.
Three positive integers x, y and z are in | Progression | CAT 2021 Slot 2 Shortcut Solution
Max product of 3 real numbers (KristaKingMath)
How to Find the Smallest Positive Integers x and y for an Inequality?
Find positive integers x and y such that x^2-2^y=2021.
Find the sum of positive integers x and y, satisfying x^2+y^2=8768.
CAT 2024 Quantitative Aptitude | 250+ Must-Do Quant Questions - 24
If x and y are positive integers, what is the value of DS08308
Find positive integers x and y, which satisfy a radical equation. AwesomeMath 2022|Math competition
Grade 7 Math #2.2b, Dividing negative and positive integers - Word Problems
The product of two consecutive positive integers is 342. Find the integers.
find two positive numbers whose product is 100 and whose sum is minimum
If two positive integers x and y are expressible in terms of primes, find their lcm and hcf
Find two positive integers x and y such that x + y = 60 and xy³ is maximum @EAG
[From CAT 1993] Suppose one wishes to find distinct positive integers x, y such that (x + y)/ xy is
To find least positive integers in Modulo Operations
Find integers x and y such that gcd (a, b) = a x + b y /gcd (a, b) as linear combinations of a and b
Find positive integers x, such that x^2+7x+49 is a perfect square.
Finding Positive Integer Solutions to an Equation (x+y+z=xyz)
The number of ordered triplets of positive integers which are solution of the equation x+y+z=100 is:
FIND THE POSITIVE INTEGERS - FACTORIZATION IS THE KEY #shorts #maths #equations #integers
If x and y are positive integers, is xy even DS01425
Комментарии
 0:02:48
0:02:48
 0:16:06
0:16:06
 0:14:07
0:14:07
 0:01:50
0:01:50
 0:13:14
0:13:14
 0:02:29
0:02:29
 0:05:29
0:05:29
 0:13:31
0:13:31
 0:56:41
0:56:41
 0:03:07
0:03:07
 0:22:00
0:22:00
 0:06:14
0:06:14
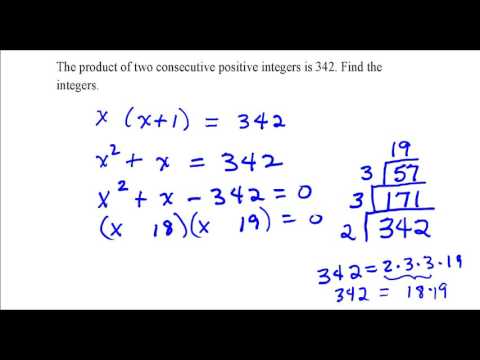 0:03:49
0:03:49
 0:03:58
0:03:58
 0:00:46
0:00:46
 0:07:43
0:07:43
![[From CAT 1993]](https://i.ytimg.com/vi/0mkid2TrjtI/hqdefault.jpg) 0:07:41
0:07:41
 0:09:36
0:09:36
 0:11:22
0:11:22
 0:05:36
0:05:36
 0:09:19
0:09:19
 0:03:43
0:03:43
 0:00:08
0:00:08
 0:04:43
0:04:43