filmov
tv
find two positive numbers whose product is 100 and whose sum is minimum
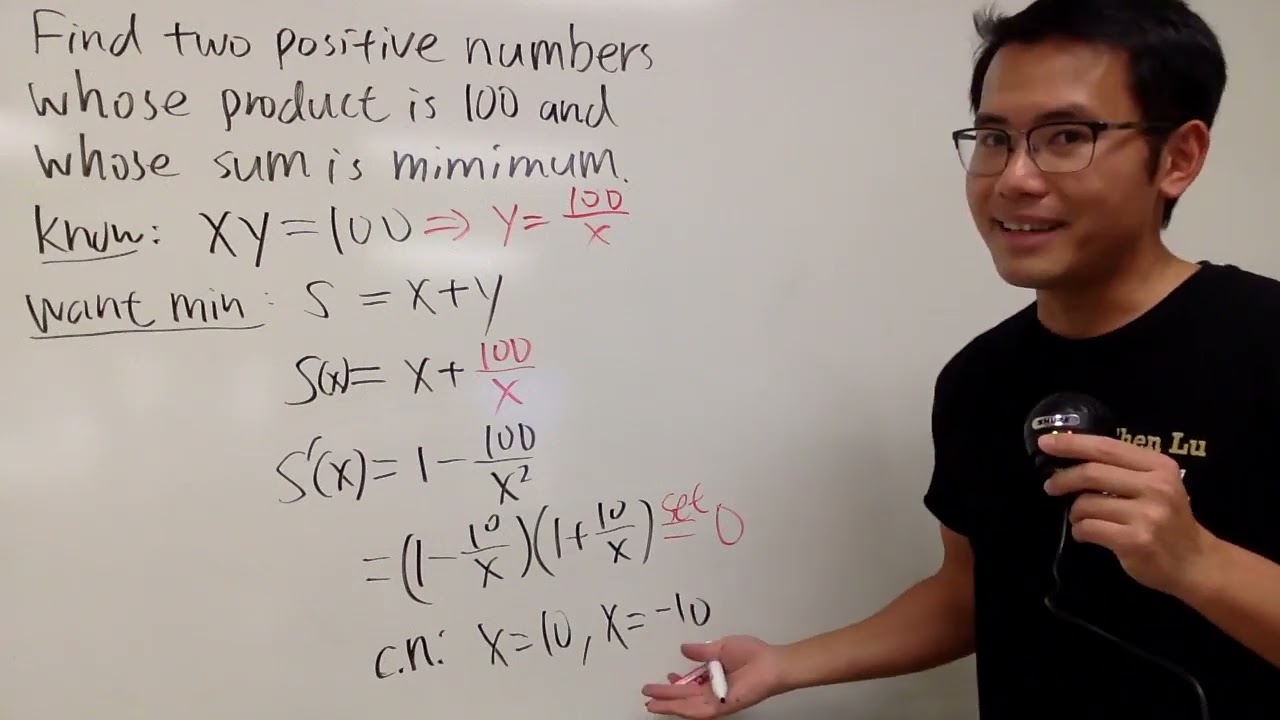
Показать описание
find two positive numbers whose product is 100 and whose sum is minimum, calculus optimization
Use "WELCOME10" for 10% off
Subscribe for more precalculus & calculus tutorials 👉 @just calculus
-------------------
If you find this channel helpful and want to support it, then you can
join the channel membership and have your name in the video descriptions:
buy a math shirt or a hoodie (10% off with the code "WELCOME10"):
-------------------
😊 Thanks to all channel members 😊
Seth Morris Andrea Mele John Calculus Maths Class
---------------------------------------------------------
---------------------------------------------------------
Best wishes to you,
#justcalculus
Use "WELCOME10" for 10% off
Subscribe for more precalculus & calculus tutorials 👉 @just calculus
-------------------
If you find this channel helpful and want to support it, then you can
join the channel membership and have your name in the video descriptions:
buy a math shirt or a hoodie (10% off with the code "WELCOME10"):
-------------------
😊 Thanks to all channel members 😊
Seth Morris Andrea Mele John Calculus Maths Class
---------------------------------------------------------
---------------------------------------------------------
Best wishes to you,
#justcalculus
find two positive numbers whose product is 100 and whose sum is minimum
Find two positive numbers whose product is 100 and whose sum is a minimum. Optimization
Optimization. Find two positive numbers whose Product is 100 and whose Sum is a Minimum.
Find two positive numbers whose squares have the difference 48 and the sum of the numbers is 12.
Find two positive numbers whose squares have the difference 48 and the sum of the numbers is 12.
Maximum product from two numbers that sum to 18
Find two positive numbers whose product is 64 And Sum is a Minimum
P WV Find two positive numbers whose sum is 16 and the sum of whose...
Number representation of binary system || Digital full course || All about vlsi ||
Find two positive numbers a and b whose AM and GM are 34 and 16 respectively.
Find two positive numbers whose product is 49 and the sum is minimum.
Find two positive numbers whose sum is 16 and the sum of whose squa...
How to find two positive numbers whose product is 100 and their sum is a minimum
Find Two Positive Numbers Where The Sum is 192 And The Product is a Minimum
Find two positive numbers whose difference is 12 and whose A.M. exceeds G.M. by 2.
Find two positive numbers a and b, whose (i) AM = 25 and GM = 20 (ii) AM = 10 and GM = 8.
Optimization: Find Two Numbers Whose Product is a Minimum
Find two positive numbers whose product is 49 and their sum is minimum. W
Find two positive numbers whose sum is 110 and whose product is a maximum. (a) Analytically complet…...
Find two positive numbers whose product is 20 and their sum is minimum | Ex 7.8.2
XI Sequence and series Find two positive numbers whose difference is 12 and whose A M exceeds the G
Find two positive numbers whose difference is 12 and whose A.M. exceeds the G.M. by 2 .
16.Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Find minimum product of two numbers with difference of 9
Комментарии
 0:03:58
0:03:58
 0:05:34
0:05:34
 0:08:23
0:08:23
 0:02:33
0:02:33
 0:03:30
0:03:30
 0:06:31
0:06:31
 0:02:46
0:02:46
 0:02:27
0:02:27
 0:35:56
0:35:56
 0:01:45
0:01:45
 0:06:42
0:06:42
 0:04:33
0:04:33
 0:02:23
0:02:23
 0:05:55
0:05:55
 0:06:22
0:06:22
 0:05:33
0:05:33
 0:04:08
0:04:08
 0:06:05
0:06:05
 0:00:33
0:00:33
 0:05:53
0:05:53
 0:04:23
0:04:23
 0:07:55
0:07:55
 0:03:55
0:03:55
 0:04:52
0:04:52