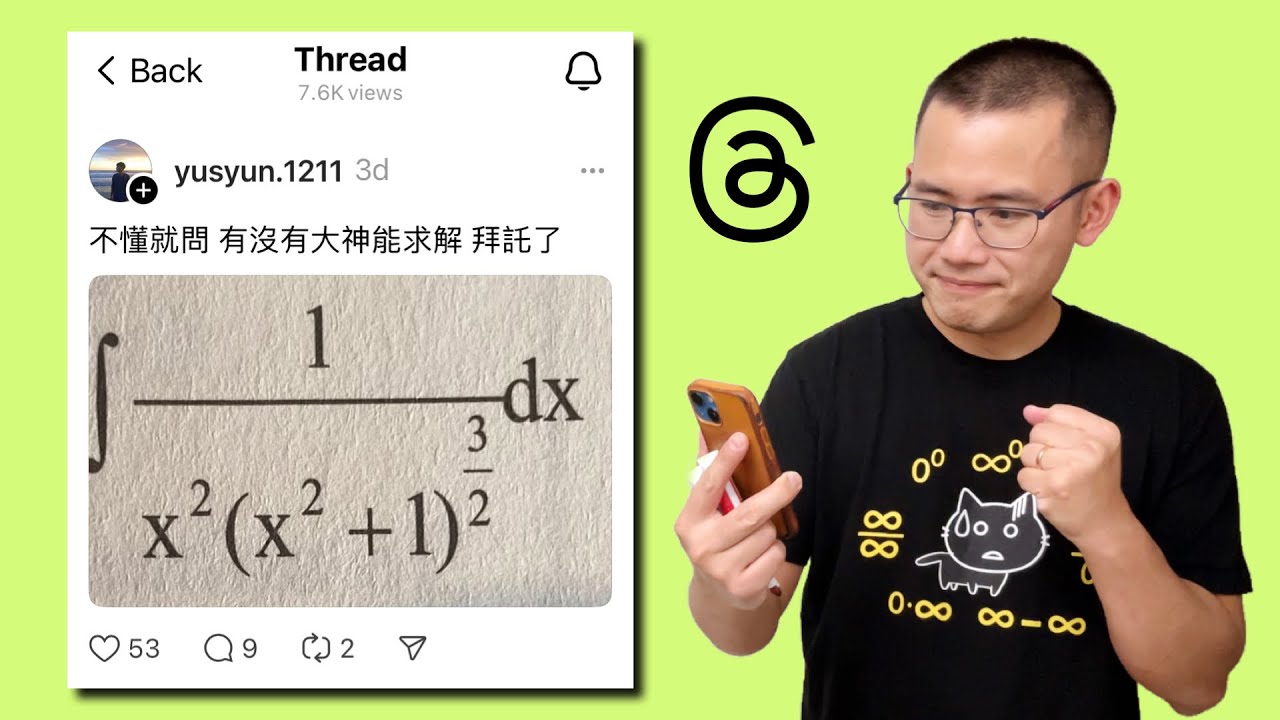
Helping you with the integral of 1/(x^2*(x^2+1)^(3/2)) using trigonometric substitution, Calculus 2

-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #maths

[kingbeauregard]

About the "+ C", maybe teach from early days that the solution to every antiderivative has two parts: the homogeneous solution and the particular solution. For antiderivatives, the homogeneous solution is always "C", since it answers the question: "what, if we take the derivative of it, is always zero?" But we're typically more interested in the particular solution, so we spend all our time working on just the particular solution. At the very end, the complete answer is the sum of the particular solution and the homogeneous solution, and THAT is why we include the "+ C" only at the end.

[ThePowerfulOne]

My calculus professor once said that Calculus is 90% algebra/geometry/trig and you only learn 10% of actual calculus. Still amazes me to this day!

[eboaly]

ur videos carried my math grade thank you so much🙏🙏🙏

[AverageCommentor]

if you clean up the result at the end you'll get -(2x^2+1)/(x*sqrt(x^2+1)) + C

[d-hat-vr]

In order to have the integrand after the x = tan θ substitution represent the same function as the original integrand, we can notice that the domain of the original integrand is all x ∉ 0. Constraining the allowable values of θ to -π/2 < θ < π/2 ∉ 0 gives the same range of y values.

In other words, the integrand written at 1:41 has the same area under curve as the original integrand, but with the domain -π/2 < θ < π/2 ∉ 0.

For the multiplication of powers at 2:02 to be correct, the base (sec θ in this case) must be positive, which it is in this question since sec θ is positive over the whole interval -π/2 < θ < π/2 ∉ 0. On the other hand, this would not be correct if the substitution x = tan θ were made under the assumption that the new domain would be 0 < θ < π .

[bjornfeuerbacher]

Or "simply" use the substitution u = x/sqrt(x²+1), then you will arrive directly at the integral at 4:30. ;)

[bachvaroff]

Forget'bout trig's, substitute $1 + x^2 = t^2 x^2 \\ x^2 = \frac{1}{t^2 - 1} \\ x^{-2} + 1 = t^2 \\ -2 x^{-3} dx = 2t dt$ etc. etc. 🙂

[rckthe]

can you help me doing the integral of v(arctanv) dv ?? pls i need help