filmov
tv
You need to try this integral
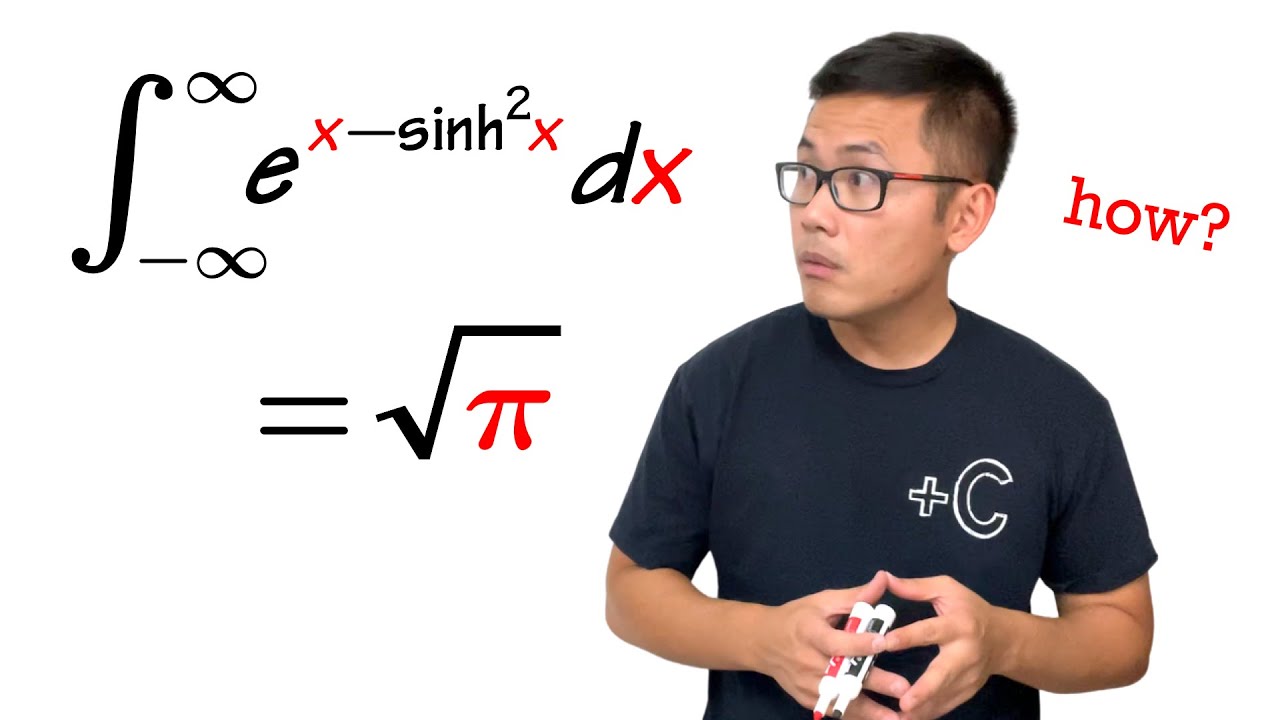
Показать описание
Evaluating a super HARD integral with an incredible shortcut: Cauchy-Schlömilch transformation.
Life from XLN Audio - You NEED to try this
You NEED to Try This 😱😳
you need to try this 🥐
YOU NEED TO TRY THIS 😂 #SHORTS
You need to try it!😋
you need to try this💀
30 ChatGPT 4o Image Generator Use Cases You Need to Try – Part 2
You NEED to Try THIS Coffee
You Need to TRY this!! #vadapav #burgerlovers #indianfood #food #shorts #snack #viralvideo #usa
You Need to Try This #ToroPartner
You Need to Try This 89% Win Rate Opening
Best Summer Fashion Trends You Need to Try #fashion
Creative apps you NEED to try 🤯💕 iPad apps | apple pencil | iPad drawing
You Need To Try This Gambit | Chess Rating Climb 1376 to 1415
Butter Bath Tomahawk Steaks (You NEED to Try This)
You need to try this with your husband 😂 #youtubeshorts #couplegoals #couple #funny #fyp #trending...
you NEED to try this glitch ASAP 🫢
15 Brilliant DIY Ideas from Genius Handyman You Need to Try
You need to try this on your friends!😭 #fortnite
5 Haircuts you NEED to try this winter… 😍🔥 (Winter Arc Haircuts)
You really need to try this!😂 #fortnite
SECRET Street Food Bread?! 🔥 You NEED To Try This NOW! #streetfood #foodie #secretrecipe? #viral
You need to try this Elevated Hair Bun!
If you’re left handed you need to try this!
Комментарии
 0:14:34
0:14:34
 0:01:06
0:01:06
 0:00:12
0:00:12
 0:00:15
0:00:15
 0:00:19
0:00:19
 0:00:18
0:00:18
 0:25:31
0:25:31
 0:00:40
0:00:40
 0:00:04
0:00:04
 0:00:22
0:00:22
 0:15:59
0:15:59
 0:00:08
0:00:08
 0:00:22
0:00:22
 1:09:56
1:09:56
 0:11:21
0:11:21
 0:00:32
0:00:32
 0:00:07
0:00:07
 0:16:06
0:16:06
 0:00:22
0:00:22
 0:00:34
0:00:34
 0:00:15
0:00:15
 0:00:06
0:00:06
 0:00:14
0:00:14
 0:00:16
0:00:16