filmov
tv
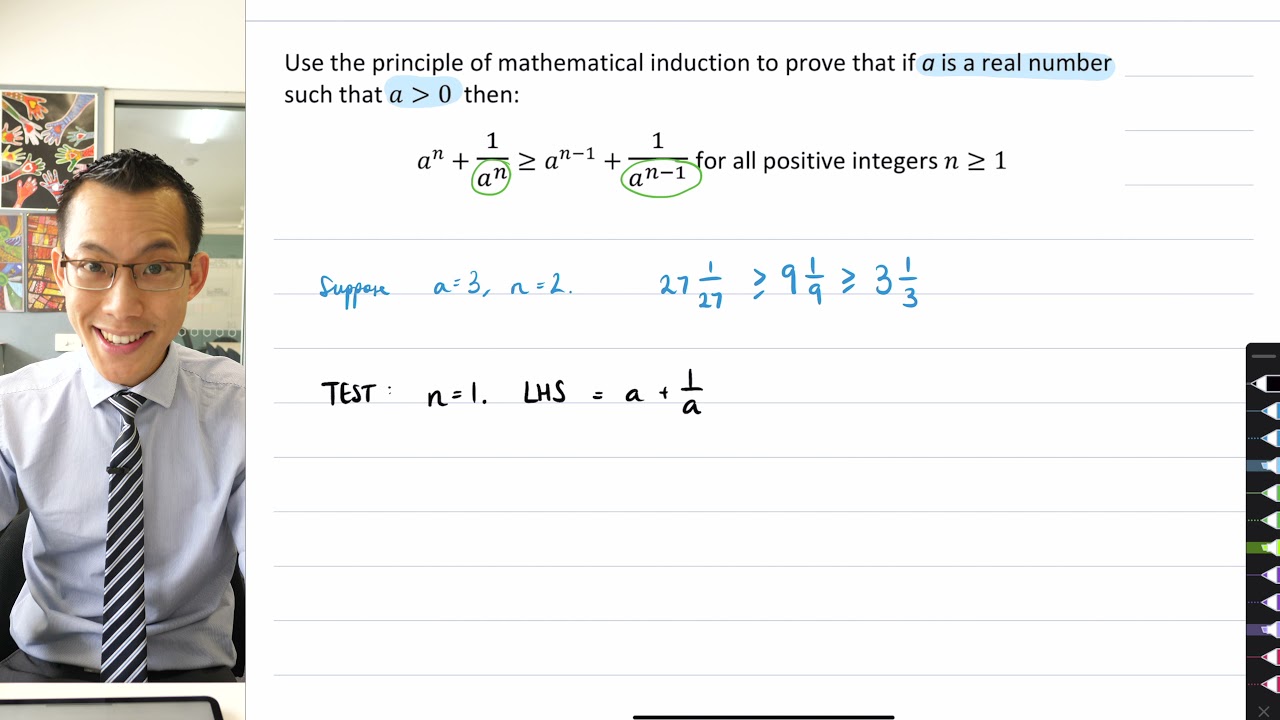
Unusual Induction Inequality Proof (1 of 3: Base case)
Показать описание
Unusual Induction Inequality Proof (1 of 3: Base case)
Induction Inequality Proofs (1 of 4: Unusual properties of inequalities)
Induction: Inequality Proofs
Induction with inequalities
Unusual Induction Inequality Proof (2 of 3: Working from the assumption)
Unusual Induction Inequality Proof (3 of 3: By exhaustion)
A-Level Further Maths: A1-26 Proof by Induction: Inequality Example 1
💯 The Inequality Proof using the Difference by Mathematical Induction. Watch this video to find out!...
LC HL proof by induction - inequality proofs
Induction Proofs Involving Inequalities.
Induction Inequality Proof: 3^n is greater than or equal to 2n + 1
Induction Inequality Proof Example 7: 4^n ≥ 1+3n
Induction Inequality Proof
Inequality Mathematical Induction Proof: 2^n greater than n^2
Proof by Induction - Inequalities
#16 proof prove induction 3^n less than n+1! inequality induccion matematicas mathgotserved
Proof by Induction: Example with Inequality
Proof by Induction (Inequality)
Mathematical Induction - Inequalities (1 of 4: General pointers)
Proof by Mathematical Induction (2 of 2: Using expression that is more restrictive to prove n=k+1)
The Principle of Mathematical Induction Inequality PROOF problem ! ! ! ! !
Proof of the GENERALIZED Inequality - Interesting Induction Method
Salsa Night in IIT Bombay #shorts #salsa #dance #iit #iitbombay #motivation #trending #viral #jee
Induction Inequality Proofs (2 of 4: Considering one side of the inequality)
Комментарии
 0:12:11
0:12:11
 0:12:23
0:12:23
 0:14:30
0:14:30
 0:04:07
0:04:07
 0:14:15
0:14:15
 0:11:10
0:11:10
 0:08:34
0:08:34
 0:08:54
0:08:54
 0:14:11
0:14:11
 0:06:34
0:06:34
 0:08:49
0:08:49
 0:09:39
0:09:39
 0:17:54
0:17:54
 0:09:20
0:09:20
 0:05:32
0:05:32
 0:12:47
0:12:47
 0:08:43
0:08:43
 0:07:17
0:07:17
 0:04:52
0:04:52
 0:09:01
0:09:01
 0:13:46
0:13:46
 0:10:11
0:10:11
 0:00:14
0:00:14
 0:08:10
0:08:10