Related Rates - Lighthouse Problem (Applications of Calculus)

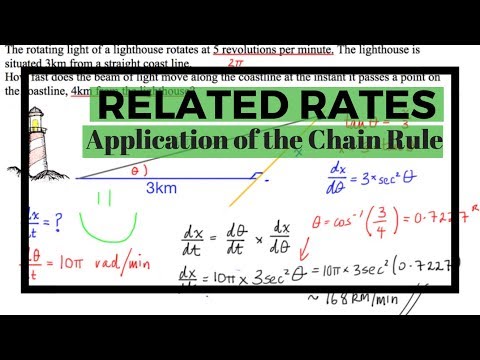
The rotating light of a lighthouse rotates at 5 revolutions per minute. The lighthouse is situated 3km from a straight coast line.
How fast does the beam of light move along the coastline at the instant it passes a point on the coastline, 4km from the lighthouse?

So here we have a related rates problem. What we are asked is determine the change in distance with respect to the change in time. To do this we are going to find the changing distance with respect to the changing angle as well as the changing angle and with respect to the changing time.

The first thing hopefully you should identify is the rate of change of angle with respect to time that can be taken from the five revolutions per minute information contained within the question. So, from this we can say that the changing angle with respect to time is equal to 10 pi radians per minute.

The next step would be to link the distance that the light travels along the beach to the angle that the light makes. We can do this by using the trigonometric ratio, the tangent and use it to set up the formulae tan(theta)=x/3, rearranging for x yields, x=3*tan(theta).

We need to differentiate this formula which yields; dx/d(theta)=3*sec^2(theta)

I hope the video helps :)

1) CHAIN RULE: You need the chain rule to take the derivative when you have a function inside a function, or a "composite function". For example, in the equation y = (3x + 1)^7, since the function 3x+1 is inside a larger, outer function, the power of 7, you will need the chain rule to find the correct derivative. How do you use the chain rule? You can think of the chain rule as the "OUTSIDE-INSIDE" rule: take the DERIVATIVE of JUST the OUTSIDE function first, LEAVING THE INSIDE FUNCTION alone (unchanged), and then MULTIPLY BY the DERIVATIVE of JUST the INSIDE function. Sometimes you might hear this expressed as: take the derivative of the outer function, "evaluated at the inner function", times the derivative of just the inner function. For our example, first take the derivative of the outer function (the power of 7) to get 7*(3x + 1)^6 since the power rule tells you that to take the derivative of a power you bring down the power to the front (as a constant or coefficient just multiplied in the front) and then you decrease the power by 1, which leaves a power of 6. Notice that you leave the inside function the way it is and just rewrite it for now. Then you multiply by the derivative of just the inner function, 3x + 1. Since the derivative of 3x + 1 is just 3, the full derivative (dy/dx) is: 7*[(3x + 1)^6]*3, which is just 21(3x + 1)^6.

1b) HOW do you know WHEN TO USE the chain rule? If the original equation had just been x^7, there would be no need for the chain rule. It's when you have something more than just x inside that you should use the chain rule, such as (3x + 1)^7 or even (x^2 + 1)^7. Sometimes the chain rule may make no difference. For instance, if you have the function (x + 1)^7, taking the derivative of the inside function just gives you 1, so multiplying by that inside derivative of 1 will not change the overall answer. However, it can't hurt to use the chain rule anyway, so it's a good idea to get in the habit of using it so that you don't forget it when it really does make a difference.

3) TRIG EXAMPLE: the idea is the same as above even if you are using the chain rule to differentiate something like a trigonometric function. If you have anything more than just x inside the trig function, you will need the chain rule to find the derivative. For the equation y = sin(x^2 - 3x), you first take the derivative of the outer function, just the sine function. Since the derivative of sine is cosine, the outside derivative (with the inside left unchanged) is cos(x^2 - 3x). Then, find the derivative of just the inside (of just the x^2 - 3x part), and multiply by that. Since the derivative of x^2 - 3x is 2x - 3, the full derivative answer is dy/dx = cos(x^2 - 3x)*(2x - 3).

3b) FORMULA: Although it's easier to think about the chain rule as the "outside-inside rule", if for any reason you have to use the formal chain rule formula, check out the two versions I show here. Both are based on the equation being a composition of functions, f(g(x)). The second version shown uses Liebniz notation. Either way, both show a component of the derivative that comes from the inside function, and it's important not to forget to multiply by this inside derivative factor if you want to get the right full derivative answer.

[jamielinsdell]

Why isn't the sine function used since the hypotenuse of 4km also ties the x value to an angle. You use the tan function without an explanation. Is it associated with the constant value of 3km from the lighthouse rather than the 4km point from the lighthouse. Depending on which trig function is used gives very different results.

[johnnolen]

Mr. Walden: Why was it necessary to get a decimal approximation for θ? Toward the end of your solution you specified θ = Arccos(3/4). It should be apparent by inspection then that sec(Arccos(3/4)) = 4/3. If you then square this result you get 16/9 as the exact value of sec^2 θ. 10π * 3 * 16/9 = 160π/3 [km/min] ∎ I don't mean to be critical, maybe there's pedagogical value in calculating an approximation first. To me though the exact value seemed obvious in this case.