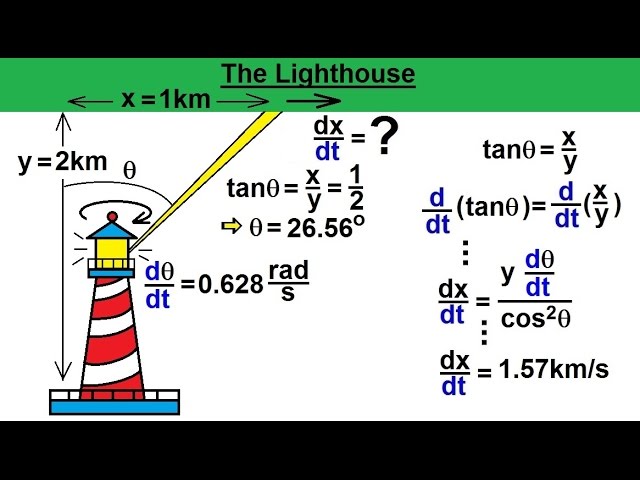
Calculus 1 - Derivatives and Related Rates (21 of 24) The LightHouse dx/dt=?

I this video I will calculate the velocity (dx/dt=?) of the light from the lighthouse as it moves across the shoreline.

Next video in this series can be seen at:

[mrbriansu]

The viewers should memorize the derivative of tan(x) is the square of sec(x) 🙂

[matricmasterclass]

HI Michel

Quick question could you use angular velocity equations to solve this problem?

[natnaelberhanu-iw]

Could it have been possible to derive tan with respect to t without writing the equivalent form of tan?

[blue_blue-]

Hi Mr. van Biezen,
I met a guy with nickname Nick… and Duck… on commenting blackpenredpen´s video „Related rates, angle increases, area increases."
He says, you are incorrect in leaving out rad in the result.
He is quite ignorant and insulting, obviously not able to understand the definition of radians.
I stopped talking to him recently.
He states, that rad can be omitted in calculus1, but not in calculus3.
What would you answer him? Could you do a video or do you know about one, which explains the properties of rad? 
Very interesting would be, how radians scale eventually pops up, if you force (d/dx)sin x to be cos(x), not knowing what this factor will be at the beginning.

[ptyptypty]

at THETA = 90 degree... we have dx/dt = (drum roll please...) INFINITY!! wow.. that's fast!! :D ....