filmov
tv
Cauchy Residue Theorem, Introduction
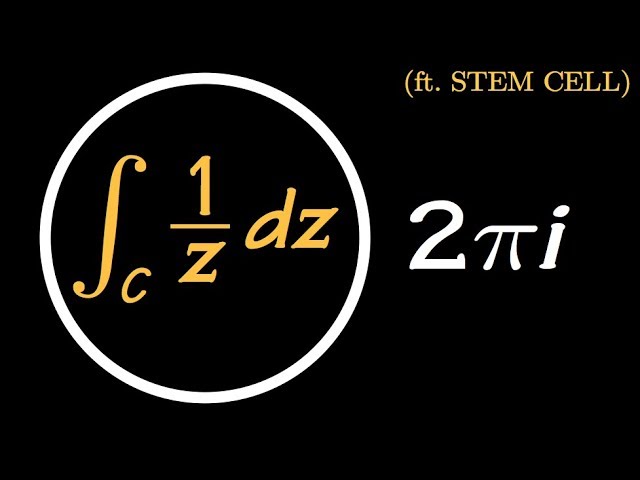
Показать описание
In this video, Will from Stem Cell showed us how to integrate the integral of 1/z over a closed contour. (yes, he will also talked about the Cauchy Residue Theorem) #CauchyResidueTheorem
Please subscribe for more math content!
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Cauchy Residue Theorem, Introduction
Complex integration, Cauchy and residue theorems | Essence of Complex Analysis #6
Complex Analysis: Residue Theorem Proof
Cauchy's Residue Theorem with Examples | Complex Integration | Complex Analysis #16
Complex Analysis 34 | Residue theorem
Residue Theorem and Proof
Basic Complex Analysis - Unit 3 - Lecture 4 - Cauchy's Residue Theorem
Cauchy Residue Theorem Introduction
Cauchy's Residue Theorem - Complex Analysis By a Physicist
Complex Analysis L09: Complex Residues
Cauchy's Residue Theorem with Proof | Complex Analysis #17
Lecture 9 - Theory of Residues & Applications Part1
Cauchy residue theorem & extended formula of residue
The residue theorem part 1 | Complex Analysis | LetThereBeMath |
Complex Analysis - Cauchy's Residue Theorem & Its Application by GP
Complex Analysis L10: Cauchy Integral Formula
Cauchy's Residue Theorem | Residue Theorem | Analytic functions | Isolated Singularities
Basic Complex Analysis - Unit 3 - Lecture 17 - Residue Calculation at Simple Pole
Evaluating Real Integrals With Cauchy's Residue Theorem - Complex Analysis By A Physicist
Complex Analysis | Unit 2 | Lecture 13 | Example of Cauchy's Integral Formula
Cauchy residue theorem|Statement and Proof|Complex Analysis|Theta Classes
Inverse Laplace Transform Using The Residue Theorem
Cauchy's ResidueTheorem
Concept of Residues with Examples - Complex Integration - Engineering Mathematics 4
Комментарии
 0:08:14
0:08:14
 0:40:45
0:40:45
 0:14:53
0:14:53
 0:10:16
0:10:16
 0:08:26
0:08:26
 0:07:03
0:07:03
 0:01:55
0:01:55
 0:11:35
0:11:35
 0:10:02
0:10:02
 0:24:51
0:24:51
 0:10:10
0:10:10
 0:57:02
0:57:02
 0:20:13
0:20:13
 0:07:54
0:07:54
 0:20:45
0:20:45
 0:16:43
0:16:43
 1:20:56
1:20:56
 0:02:30
0:02:30
 0:16:06
0:16:06
 0:09:05
0:09:05
 0:42:22
0:42:22
 0:04:24
0:04:24
 0:17:24
0:17:24
 0:08:33
0:08:33