filmov
tv
let G be a group & x be an element of odd order in G then for any element y in G their exist y^2=x
Показать описание
in this leacture we will learn about group.
1) cube root of unity is a group under multiplication, (G,*) is a group where G = ( 1, w, w^2).
2) show that S={2^n : n ∈ z } form a group under multiplication.
3) M2 be the set of all upper triangular 2 by 2 non singular matrice from a group under multiplication.
4) show that the set S = ( a+b√2: a,b ∈ Q ) form a group under multiplication.
5) the set S = ( xi + 0j : x ∈ R ) of vector in Euclidean plane form a group under addition.
6) Group theory, prove that the nth roots of unity forms an abelian group under multiplication.
7) Group theory, prove that the set of 2 by 2 matrices form an abelian group under multiplication.
8) Group theory, prove that G = ( 1, -1, i, -i ) forms an abelian group under multiplication.
9) let g be an element (non-identity) of a group G then g is its own inverse iff g is of order 2.
10) let g1g2 be two elements of a finite group G, then the order of g1g2 is the same as that of g2g1.
11) Group theory, prove that the order of an element g in G is equal to the order of its inverse.
12) Group theory, if every non- identity element of a group has order 2 then G is an abelian group.
13) Group theory, prove that every cyclic group is abelian.
14) Group theory, Every group of prime order is cyclic.
15) Group theory, two step subgroup test, two step test for subgroup.
16) Group theory, prove that Intersection of two subgroup of group G is subgroup.
17) Group theory, prove that Center of a group is subgroup of G.
18) Group theory, If H is a subgroup of G then aHa^-1 (conjugate of subgroup) is also a subgroup.
19) Group theory, If H and K are two subgroup of a group G whose order is relatively prime then H∩K=e.
20) Group theory, prove that any two right cosets are either disjoint or identical.
21) Group theory, state and prove Lagrange's theorem // Lagrange's theorem.
22) Let H be a subgroup of a group G then quotient set 𝐆/𝐇={𝒈𝑯 :𝒈∈𝑮} form a group under multiplication.
23) Isomorphism ll Show that mapping 𝝍:(𝑹×𝑹,+)→{𝑽_𝟐 (𝑹),+} define by 𝝍(𝒙,𝒚)=𝒙𝒊 +𝒚𝒋 is an isomorphism.
24) Group theory, prove that Every infinite cyclic group is isomorphic to group ( z, +) of all integers.
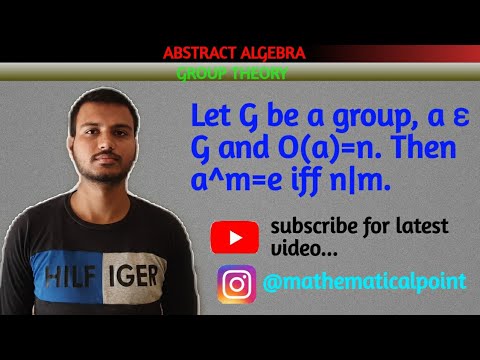
25) Group theory, prove that the order of an element of a group divides the order of group G.
26) let G be a group & x be an element of odd order in G then for any element y in G their exist y^2=x.
1) cube root of unity is a group under multiplication, (G,*) is a group where G = ( 1, w, w^2).
2) show that S={2^n : n ∈ z } form a group under multiplication.
3) M2 be the set of all upper triangular 2 by 2 non singular matrice from a group under multiplication.
4) show that the set S = ( a+b√2: a,b ∈ Q ) form a group under multiplication.
5) the set S = ( xi + 0j : x ∈ R ) of vector in Euclidean plane form a group under addition.
6) Group theory, prove that the nth roots of unity forms an abelian group under multiplication.
7) Group theory, prove that the set of 2 by 2 matrices form an abelian group under multiplication.
8) Group theory, prove that G = ( 1, -1, i, -i ) forms an abelian group under multiplication.
9) let g be an element (non-identity) of a group G then g is its own inverse iff g is of order 2.
10) let g1g2 be two elements of a finite group G, then the order of g1g2 is the same as that of g2g1.
11) Group theory, prove that the order of an element g in G is equal to the order of its inverse.
12) Group theory, if every non- identity element of a group has order 2 then G is an abelian group.
13) Group theory, prove that every cyclic group is abelian.
14) Group theory, Every group of prime order is cyclic.
15) Group theory, two step subgroup test, two step test for subgroup.
16) Group theory, prove that Intersection of two subgroup of group G is subgroup.
17) Group theory, prove that Center of a group is subgroup of G.
18) Group theory, If H is a subgroup of G then aHa^-1 (conjugate of subgroup) is also a subgroup.
19) Group theory, If H and K are two subgroup of a group G whose order is relatively prime then H∩K=e.
20) Group theory, prove that any two right cosets are either disjoint or identical.
21) Group theory, state and prove Lagrange's theorem // Lagrange's theorem.
22) Let H be a subgroup of a group G then quotient set 𝐆/𝐇={𝒈𝑯 :𝒈∈𝑮} form a group under multiplication.
23) Isomorphism ll Show that mapping 𝝍:(𝑹×𝑹,+)→{𝑽_𝟐 (𝑹),+} define by 𝝍(𝒙,𝒚)=𝒙𝒊 +𝒚𝒋 is an isomorphism.
24) Group theory, prove that Every infinite cyclic group is isomorphic to group ( z, +) of all integers.
25) Group theory, prove that the order of an element of a group divides the order of group G.
26) let G be a group & x be an element of odd order in G then for any element y in G their exist y^2=x.
0:09:08
Lecture 15 | Let G be a group then orders of the element of G and its inverse are same
0:09:13
Let G be a group ; then o(a)|o(G) for an element a in G.
0:11:01
Let G be group, a ɛ G and O(a)=n. Then for any positive integer k, O(a^k) =n/(n,k).
0:07:08
If G be a Group,then (ab)'=b'a' /Group Theory/3rd sem/unit-1/Telugu expalination
let G be a group & x be an element of odd order in G then for any element y in G their exist y^2...
0:05:35
Groups - Showing G is a group - Part 1
0:09:48
Let G be a group, a ɛ G and O(a)=n. Then a^m=e iff n|m.
0:06:35
let G be a group and a belong to a to G has infinite order, then all distinct power of the a are
0:10:16
Let G be a group and let Z(G) be the center of G. If G/Z(G) is cyclic, then G is Abelian.
0:01:25
GATE CS 2014 Set 3 | Question: 3 Let G be a group with 15 elements. Let L be a subgroup of G.
0:12:45
Group Theory | Let G be group of even order prove that at least one element of order 2? | Pure math
0:04:53
Lecture 18 | Let G be a group and x be an element of odd order in G then for any y in G y^2 =x exist
0:02:03
Let G be the simple group of order 168.What is the number of subgroup of G of order 7
0:18:44
Let G be cyclic group of order n then a_k is generator of G if gcd(k, n)=1
0:09:56
Proof that f(a) = a^(-1) is a Group Isomorphism if G is Abelian
0:03:23
Groups of Prime Order p are Cyclic with p-1 Generators Proof
0:06:45
Let G be a group and Phi an automorphism of G. If a in G has order o(a), then o(phi(a)) is o(a) .
0:02:26
GATE 2020 CS Q18. Let G be a group of 35 elements.Then the largest possible size of subgroup SOLVED!
0:11:42
Group theory, prove that G = ( 1, -1, i, -i ) forms an abelian group under multiplication
0:11:34
Let G be a group ab=ac prove that b=c and ba=ca prove that b=c || group therory | Hindi,Urdu |
0:00:59
#24 Let G be a group and a be an element of order 30 in G then the order of a^18 is | UPTGT 2004
0:02:49
AKPotW: Showing that the group generated by an element of G is a subgroup of G [Algebra]
0:08:21
Let G be a cyclic group order n generated by a...(B.sc Group theory Theorem)
0:06:30
let g be an element (non-identity) of a group G then g is its own inverse iff g is of order 2
Комментарии