A Non-Archimedean Definable Chow Theorem

Speaker: Abhishek Oswal
Affiliation: IAS
11/20/20

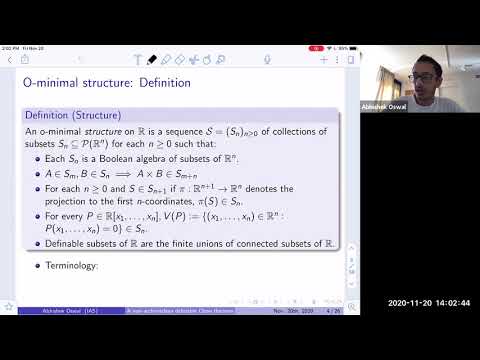
Algebraization theorems originating from o-minimality have found some surprising applications in Diophantine geometry and Hodge theory. One such key result is the 'definable Chow theorem' of Peterzil and Starchenko which states that every closed analytic subset of a complex algebraic variety that is also definable an o-minimal structure, is in fact an algebraic subset. This talk will be about a non-archimedean analogue of this result.