Christian Dahlhausen - Continuous K-theory and K-theory of Zariski-Riemann spaces

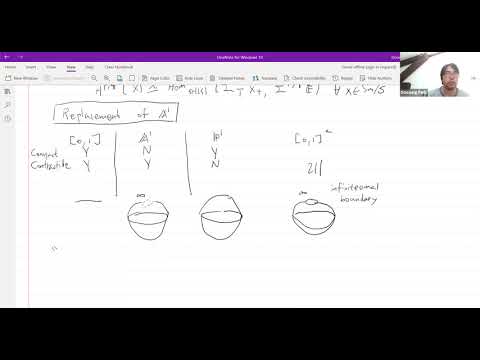
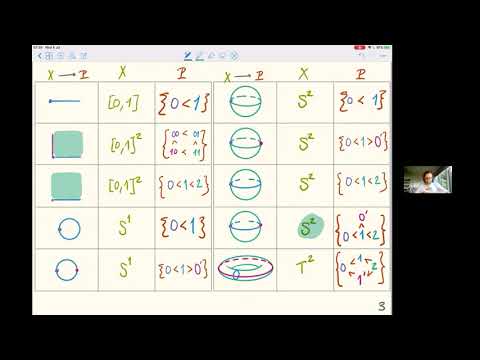
Continuous K-theory is a derivative of algebraic K-theory for rigid analytic spaces, it was defined by Morrow and further studied by Kerz-Saito-Tamme. This talk will be an introduction to the subject. First we define continuous K-theory for Tate rings (e.g. affinoid algebras over some complete discretely valued field) and then we use pro-cdh descent (by Kerz-Strunk-Tamme) to see that it satisfies descent for the admissible topology on the category of rigid spaces so that it is defined globally. In the spirit of Raynaud's description of rigid spaces it is fruitful to study the continuous K-theory of a rigid space in terms of the continuous K-theory of all its integral formal models; this yields us to study the K-theory of (relative) Zariski-Riemann spaces which behaves similar to the K-theory of regular schemes (essentially due to Raynaud-Gruson's "platification par eclatement"). In the end, I will state some results about negative continuous
K-theory. References:

- Morrow: A historical overview of pro cdh descent in algebraic K-theory and its relation to rigid analytic varieties (arXiv:1612.00418).

- Kerz-Saito-Tamme: K-theory of non-archimedean rings I. Doc. Math. 24, 2019 (arXiv:1802.09819).

- Dahlhausen: Continuous K-Theory and Cohomology of Rigid Spaces (arXiv:1910.10437).