O-Minimality and Hodge Theory: Definable GAGA + Griffiths Conjecture

Speaker: Jacob Tsimerman
Affiliation: Toronto
11/17/20

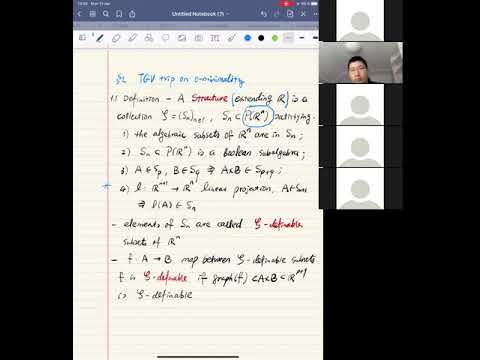
In this pair of lectures, we will explain how to develop an o-minimal geometry allowing for nilpotents, that we call "definable analytic spaces". We explain how to use this theory to prove a definable GAGA statement, and how one can use this to prove a conjecture of Griffiths that the images of period maps are algebraic. We will also discuss the analogous o-minimal in the setting of variations of mixed Hodge structures, and a generalization of Griffiths conjecture to this setting.