Definability of Berkovich curves

By Jerôme Poineau (Caen)
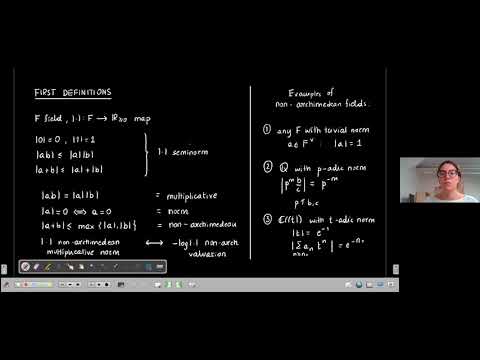
Abstract: Hrushovski and Loeser recently introduced a model-theoretic version of the analytification of a quasi-projective variety over a non-archimedean valued field. It gives rise to a strict pro-definable set in general and to a definable set in the case of curves. We focus on the later case and provide an alternative approach to endow
the analytification of an algebraic curve with a definable structure. The main tools used are the semistable reduction theorem and Temkin’s radialization theorem (for definability of morphisms). Along the way, we give definable versions of several usual notions of Berkovich analytic geometry: branch emanating from a
6 point, residue curve at a point of type 2, etc. A merit of this approach is that we are able to leave the realm of algebraic curves and consider some analytic compact curves and analytic morphisms between them. In addition, it allows us to get a
complete description of the definable subsets of analytic curves.
This is joint work with Pablo Cubides Kovacsics.