filmov
tv
Banach Spaces part 1

Показать описание
Lecture with Ole Christensen. Kapitler: 00:00 - Banach Spaces; 06:30 - Cauchy Sequences; 12:00 - Def: Banach Space; 15:45 - Examples; 17:15 - C[A,B] Is Banach With Proof; 36:30 - Ex: Sequence Space L^1(N); 46:45 - Sequence Space L^p(N);
Banach Spaces part 1
Lecture 1: Basic Banach Space Theory
#24: Tommaso Russo- Asplund Banach spaces with norming Markuševič bases
MAST30026 Lecture 18: Banach spaces (Part 1)
Hilbert Spaces: Banach Space and Completions, 1-27-23 part 1
Some 20+ year old problems about Banach spaces and operators on them – W. Johnson – ICM2018
BANACH SPACES PART-1 _PG TRB/ POLYTECHNIC
Mini-Course: Regularization methods in Banach spaces - Class 01
Banach Space Part-1
Functional Analysis 7 | Examples of Banach Spaces
Banach spaces 1
On algebras which are inductive limits of Banach spaces
Banach Spaces - Lec02 - Frederic Schuller
Joel FISH - 1/3 sc-Banach spaces and the sc-calculus
Guillaume Aubrun: Asymptotic tensor powers of Banach spaces
lp BANACH SPACE PART-1
Banach-valued Analysis, Lecture 4 part 1: Probability in Banach spaces
Lecture 8 (Part 1): A non example of Hilbert Space, Banach Space and example
Examples of Banach spaces (1)
Real Analysis Lecture 35 Part 1: Completion of a Normed Vector Space
Real Analysis Lectures Part 10: Banach Space C([a,b])
Semigroup of bounded linear operators on Banach space - Part 1
Functional Analysis Lecture 6 (Lp Spaces are Banach);Not compactness of the Unit Ball
M3302 - Differential Calculus in Banach spaces - Section 4.1 Definitions and examples - Part 1
Комментарии
 0:48:52
0:48:52
 1:15:19
1:15:19
 1:00:46
1:00:46
 0:49:55
0:49:55
 0:59:51
0:59:51
 0:50:59
0:50:59
 0:09:09
0:09:09
 1:18:44
1:18:44
 0:25:54
0:25:54
 0:13:04
0:13:04
 1:12:44
1:12:44
 0:50:23
0:50:23
 1:49:17
1:49:17
 1:11:50
1:11:50
 0:47:04
0:47:04
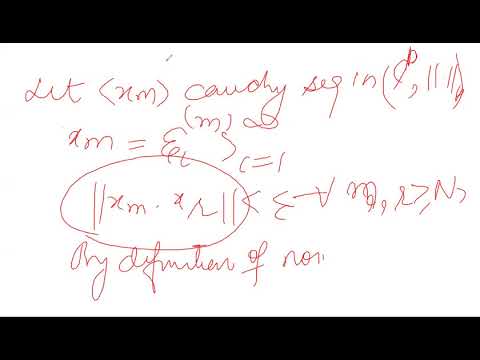 0:07:23
0:07:23
 0:45:31
0:45:31
 0:30:25
0:30:25
 1:04:38
1:04:38
 0:28:57
0:28:57
 0:30:07
0:30:07
 0:40:23
0:40:23
 0:13:00
0:13:00
 0:29:42
0:29:42