Proof of the Convolution Theorem :: Laplace Transforms

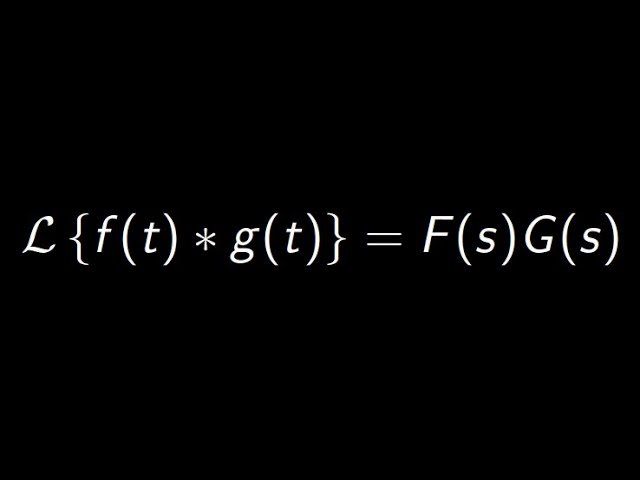
preview_player
Показать описание
Here we prove the Convolution Theorem using some basic techniques from multiple integrals.

We first reverse the order of integration, then do a u-substitution. These two techniques should be very familiar from multivariable calculus.

I hope seeing the proof of the convolution theorem helps you gain greater understanding of the idea behind why it works!

It's super easy to use and now you know why it works!

Post any questions you have below and I'll try to answer the best I can!

Thanks for watching! -j Dub
  1. Jonathan Walters
  2. Proof of the Convolution Theorem
  3. Convolution Theorem
  4. Laplace Transforms
  5. Laplace Convolution
  6. Convolution Laplace
Рекомендации по теме
Proof of the 0:18:10

Proof of the Convolution Theorem

Proof of Convolution 0:04:04

Proof of Convolution Theorem

The Convolution of 0:10:33

The Convolution of Two Functions | Definition & Properties

Proof of convolution 0:26:50

Proof of convolution Theorem bsc maths || Inverse Laplace Transform Engineering mathematics

Proof of the 0:04:35

Proof of the Convolution Theorem :: Laplace Transforms

Proof of Convolution 0:07:39

Proof of Convolution Theorem of Fourier Transform - Advanced #Calculus by #Moein

20. Convolution Theorem 0:08:41

20. Convolution Theorem for Fourier Transforms | Proof | Most Important

The convolution and 0:13:46

The convolution and the laplace transform | Laplace transform | Khan Academy

Question: Proof of 0:06:05

Question: Proof of Convolution Theorem

Convolution Theorem(Fourier transform) 0:08:09

Convolution Theorem(Fourier transform)

The Convolution Theorem 0:00:08

The Convolution Theorem | State and prove Convolution Theorem | The Convolution operation |

Proof of Convolution 0:04:52

Proof of Convolution Theorem | LTI Systems

Laplace Transform | 0:16:55

Laplace Transform | Convolution Theorem | Concept & Example by GP Sir

Convolution || State 0:11:49

Convolution || State and prove convolution theorem || INVERSE LAPLACE TRANSFORM | BSc Mathematics

Video5-18: Convolution Theorem, 0:22:22

Video5-18: Convolution Theorem, proof, examples, application. Elementary differential equations

Convolution theorem | 0:06:31

Convolution theorem | Quick & Easy proof.

Statement and proof 0:18:35

Statement and proof of Convolution theorem, lecture-15, Laplace transformation

convolution theorem || 0:05:30

convolution theorem || convolution theorem fourier transform || convolution theorem proof

CONVOLUTION THEOREM || 0:28:05

CONVOLUTION THEOREM || proof of convolution theorem || laplace invers

Lecture 31-Convolution Theorem 0:30:45

Lecture 31-Convolution Theorem for Laplace Transforms-II

Fourier transform / 0:05:18

Fourier transform / Convolution Theorem for Fourier Transform with proof

Convolution Theorem Proof 0:20:50

Convolution Theorem Proof | Laplace Transform of Integrals | Changing the Order of Integration.

Convolution Theorem ||statement 0:09:30

Convolution Theorem ||statement and proof ||

Introducing Convolutions: Intuition 0:11:08

Introducing Convolutions: Intuition + Convolution Theorem

Комментарии
Автор

The exact proof was asked in our exam today, could do it just because of you, thank you

dikshaarora
Автор

This is very nice, you have explained it better than my professor. Thank you! 👍

martinxiang
Автор

anyone else looks at the sum of independent random variables differently?

MACC-gkui
Автор

So simple and concise. Thanks for making this video.

BlueEdgeTechno
Автор

Thanks for this simplified explanation

Error-tblu
Автор

on 1:48 could you please explain how could we just simply take exp(-st) in the integral and f(r) out from the integral? Is it because since we switched integral order which makes these two functions to constants so we can just move in and out in the integral?

tuntapatsirikup
Автор

Tq sir but how to use this theorem at any questions..plz help me sir...🙏🙏

divyadubey
Автор

Great job man. Very much Appreciated from India ❤️

SayandeepBMSCE