filmov
tv
Find Pivots, Pivot Rows, and Pivot Columns with Row Echelon Form | Linear Algebra
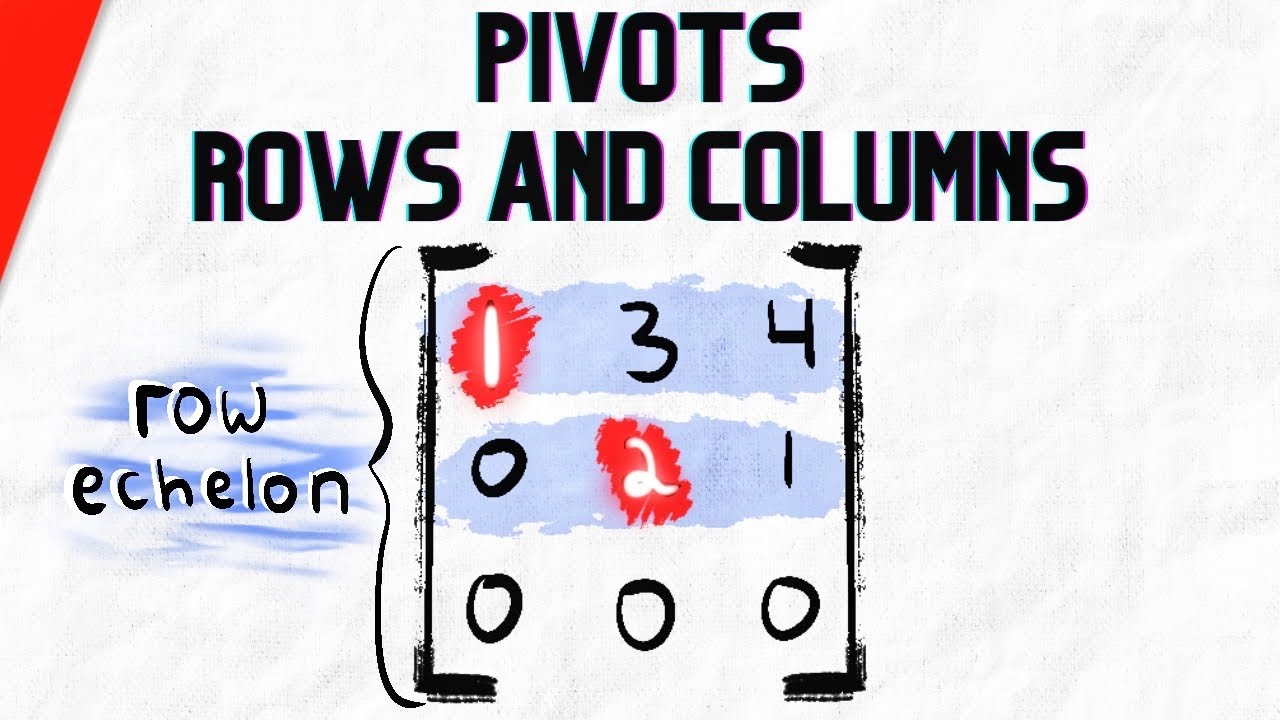
Показать описание
We go over how to find the pivot positions, pivots, pivot rows, and pivot columns of a matrix by considering its row echelon or reduced row echelon forms. #linearalgebra
Join Wrath of Math to get exclusive videos, lecture notes, and more:
The pivot positions of a matrix are the positions of the leading 1s when it is written in row echelon or reduced row echelon form. The entries of the matrix that are in these position are the pivots of the matrix. The rows containing the pivot positions are the pivot rows and the columns containing the pivot positions are the pivot columns.
★DONATE★
Follow Wrath of Math on...
Join Wrath of Math to get exclusive videos, lecture notes, and more:
The pivot positions of a matrix are the positions of the leading 1s when it is written in row echelon or reduced row echelon form. The entries of the matrix that are in these position are the pivots of the matrix. The rows containing the pivot positions are the pivot rows and the columns containing the pivot positions are the pivot columns.
★DONATE★
Follow Wrath of Math on...
Find Pivots, Pivot Rows, and Pivot Columns with Row Echelon Form | Linear Algebra
How to Find the Pivots and Pivot Columns of a Matrix From Row Echelon Form
Find Pivots and Solve System from Row Echelon Form | Linear Algebra Exercises
Row Echelon Form, Pivot Positions, Basic and Free Variables
Pivot Table Excel Tutorial
Ex: Simplex Method - Perform the Pivot Operation Given a Tableau
Dalton Caldwell - All About Pivoting
How to find pivots in Linear Algebra
You Won't Believe These Crazy PIVOT TABLE Hacks!
Echelon Forms, Pivots & Pivot Columns (Linear Algebra)
PIVOTS AND FREE VARIABLES
Excel Pivot Table EXPLAINED in 10 Minutes (Productivity tips included!)
Determine Basic (Leading) Variables and Free Variables Given a Matrix in RREF
Advanced Pivot Table Techniques (to achieve more in Excel)
MS Excel - Pivot Table Example 1 Video Tutorials
Learn Pivot Tables in 6 Minutes (Microsoft Excel)
Pivots and Pivot Columns
PIVOT - Understanding the Basics in SQL
SQL Query - Convert data from Rows to Columns | Pivot
Merging Multiple Pivot Tables In Excel #myexcelmaster
Multiple Row Filters in Pivot Tables
Find the earliest and latest calls using Pivots
Pivot tables with Pandas
Gaussian Elimination with Partial Pivoting
Комментарии
 0:05:58
0:05:58
 0:05:47
0:05:47
 0:07:36
0:07:36
 0:08:47
0:08:47
 0:13:36
0:13:36
 0:07:29
0:07:29
 0:27:55
0:27:55
 0:02:58
0:02:58
 0:11:30
0:11:30
 0:06:24
0:06:24
 0:22:54
0:22:54
 0:13:22
0:13:22
 0:02:28
0:02:28
 0:11:47
0:11:47
 0:15:05
0:15:05
 0:06:22
0:06:22
 0:01:23
0:01:23
 0:06:21
0:06:21
 0:04:56
0:04:56
 0:04:36
0:04:36
 0:02:00
0:02:00
 0:01:15
0:01:15
 0:09:00
0:09:00
 0:08:27
0:08:27