filmov
tv
Decomposing a 3D PGA Rotor
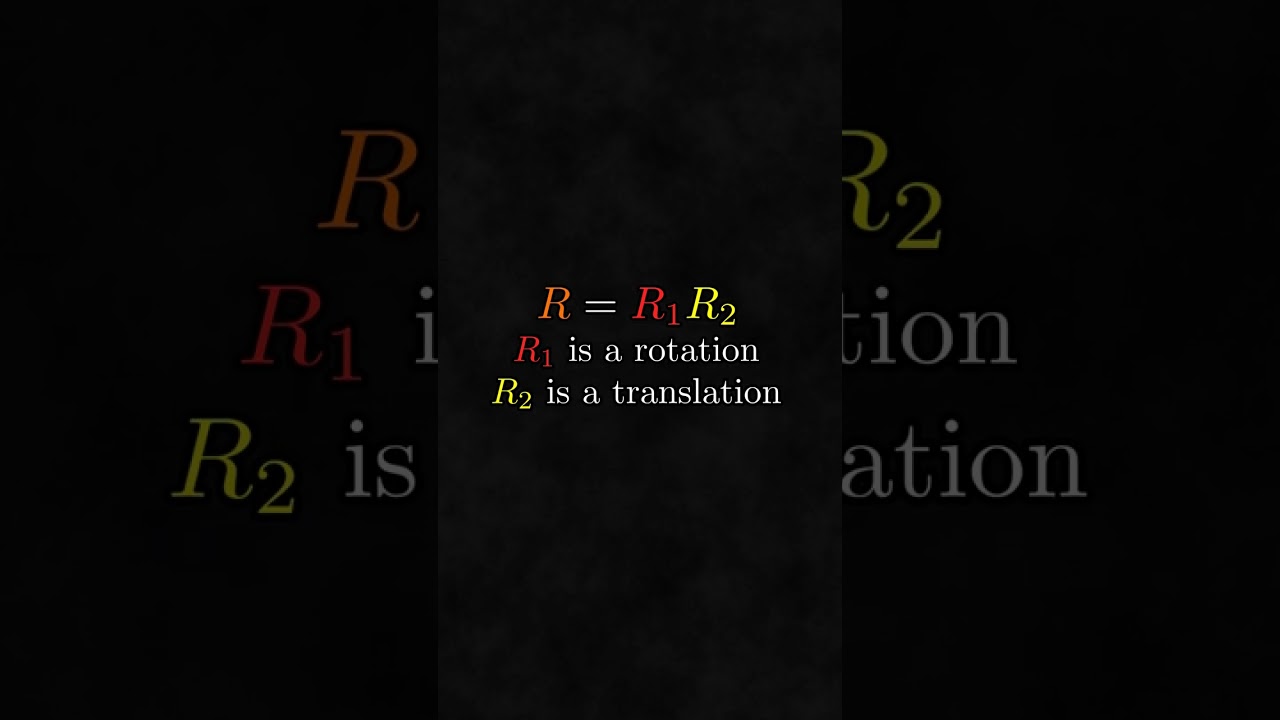
Показать описание
A couple weeks ago I talked about how to calculate the invariant decomposition of a 3D PGA bivector into simple commuting parts. But what about decomposing a 3D PGA rotor into simple commuting factors? Once again, these ideas came from Roelf and De Keninck's paper "Graded Symmetry Groups: Plane and Simple".
Supporters:
David Johnston
Jason Killian
jerrud
Richard Penner
trb
Supporters:
David Johnston
Jason Killian
jerrud
Richard Penner
trb
Decomposing a 3D PGA Rotor
Decomposition of a 3D PGA Bivector
A Swift Introduction to Projective Geometric Algebra
AGACSE2021 Martin Roelfs - Graded Symmetry Groups
GAME23 Martin Roelfs - Hidden in the Fold
GAME2020 0. Steven De Keninck. Dual Quaternions Demystified
2.7 Rotations | Geometric Algebra for Physicists
GAME23 Chris Doran - GA: Level Up!
Addendum to A Swift Introduction to Geometric Algebra
SimpleGA: A Lightweight Geometric Algebra Library | Chris Doran | JuliaCon 2023
ICACGA 2022: Improving Matrix Methods with Geometric Algebra
Ntropy Learning & Development: Introduction to Geometric Algebra
AGACSE2021 Joan Lasenby - GA approach to orthogonal transformations in signal and image processing.
ICACGA 2022: A lightweight implementation of GA in Julia
GAME23 Leo Dorst - Geometric Dynamics
ICACGA 2022: They Do It with Mirrors – The Essence of PGA
Quaternions and Clifford Algebra
GAME2020 - 1. Dr. Leo Dorst. Get Real! (new audio!)
Unified Expression Framework of Geodetic Stations Based on Conformal Geometric Algebra
AGACSE2021 Anthony Lasenby - Fundamental Forces
QED Prerequisites Geometric Algebra: Spacetime.
Geometric Algebra, First Course, Episode 06: Scalar Product and the Metric.
Geometric algebra lectures 02 - Geometric product
Rotation Dynamics of a Rigid Body with Vector Calculus and Geometric Algebra
Комментарии
 0:01:00
0:01:00
 0:00:52
0:00:52
 0:54:38
0:54:38
 1:04:54
1:04:54
 1:17:03
1:17:03
 0:48:02
0:48:02
 0:06:21
0:06:21
 1:09:45
1:09:45
 0:23:40
0:23:40
 0:31:27
0:31:27
 0:39:38
0:39:38
 0:55:11
0:55:11
 0:37:05
0:37:05
 0:43:33
0:43:33
 1:02:41
1:02:41
 0:43:46
0:43:46
 1:50:29
1:50:29
 1:55:47
1:55:47
 0:12:29
0:12:29
 1:13:57
1:13:57
 0:37:21
0:37:21
 0:49:29
0:49:29
 0:13:08
0:13:08
 0:17:00
0:17:00