filmov
tv
Summing Powers of 6 (geometric sum visualization)

Показать описание
This is a short, animated visual proof demonstrating the finite geometric sum formula for any integer n with n greater than 3 (explicitly showing the case n=6 with k=3). This series (and its infinite analog when x less than 1) is important for many results in calculus, discrete mathematics, and combinatorics.
Thanks!
#manim #math #geometricsums #series #calculus #mtbos #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #finitesums #finiteseries #geometric #mathshorts #mathvideo
To learn more about animating with manim, check out:
Thanks!
#manim #math #geometricsums #series #calculus #mtbos #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #finitesums #finiteseries #geometric #mathshorts #mathvideo
To learn more about animating with manim, check out:
Summing Powers of 6 (geometric sum visualization)
Infinite sum of powers of sixths!
Geometric Series: sum of powers of 1/6 (visual proof)
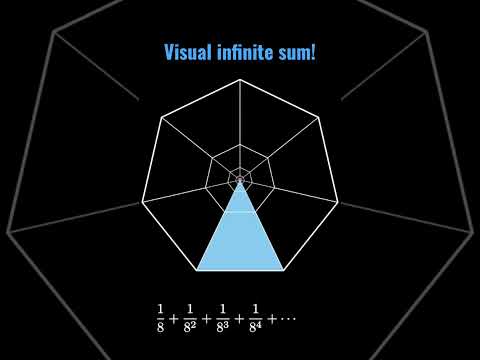
Summing powers of 1/8 visually!
Geometric sum of powers of 7
A visual infinite sum like you’ve never seen!
Infinite sum of powers of 4/9
What's this infinite sum?
Summing Powers of Three
Geometric Series: sum of powers of 1/8 (visual proof)
Geometric series: sum of powers of 1/5 (visual proof)
Geometric series: sum of powers of 1/3 (visual proof)
Geometric series: sum of powers of 1/4 (visual proof)
Geometric series: sum of powers of 1/5 II (visual proof)
Power sum MASTER CLASS: How to sum quadrillions of powers ... by hand! (Euler-Maclaurin formula)
Geometric series: sum of powers of 1/2 (visual proof)
Infinite Geometric Series Sum
Geometric Series: sum of powers of 1/9 (visual proof)
Sum of n squares | explained visually |
Geometric Series: Alternating Sum of Powers of 1/4 (visual proof)
Geometric series: sum of powers of 4/9 (visual proof)
Geometric series: sum of powers of 1/3 II (visual proof)
Geometric Series | Convergence, Derivation, and Example
Summing positive integers with triangles
Комментарии
 0:00:29
0:00:29
 0:00:55
0:00:55
 0:01:32
0:01:32
 0:00:53
0:00:53
 0:01:00
0:01:00
 0:00:57
0:00:57
 0:00:52
0:00:52
 0:00:31
0:00:31
 0:00:58
0:00:58
 0:01:13
0:01:13
 0:02:05
0:02:05
 0:01:49
0:01:49
 0:01:06
0:01:06
 0:02:04
0:02:04
 0:50:01
0:50:01
 0:01:17
0:01:17
 0:00:45
0:00:45
 0:01:41
0:01:41
 0:02:14
0:02:14
 0:01:26
0:01:26
 0:01:28
0:01:28
 0:01:18
0:01:18
 0:06:28
0:06:28
 0:00:35
0:00:35