filmov
tv
abc Conjecture - Numberphile
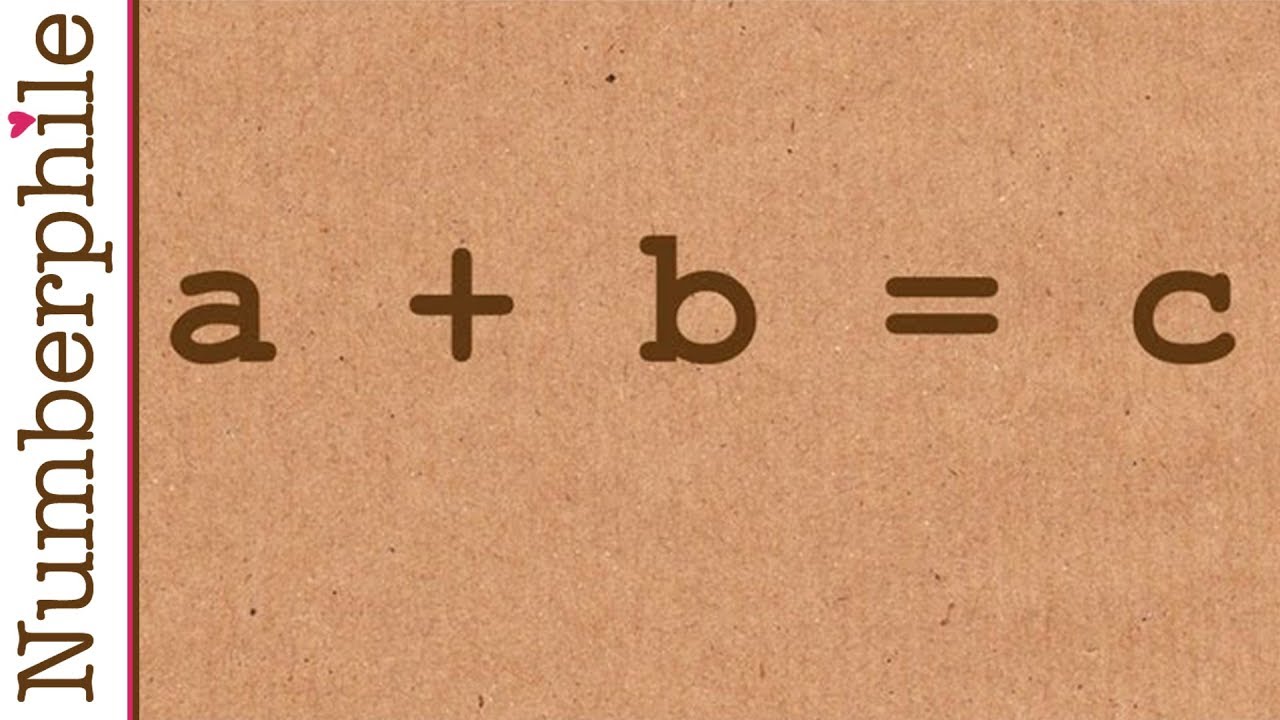
Показать описание
The abc Conjecture may have been proven by a Japanese mathematician - but what is it?
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by Brady Haran
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by Brady Haran
abc Conjecture - Numberphile
Twin Prime Conjecture - Numberphile
Poincaré Conjecture - Numberphile
The abc conjecture
Charles Hoskinson on Has the ABC conjecture been solved
Drama behind the abc conjecture #stem
ABC Intro - part 1 - What is the ABC conjecture?
The Abc Conjecture Trailer
Controversial ABC Conjecture Proof Published?!?
Find your own ABC Conjecture Triple
The ABC conjecture
The Constant to ABC Conjecture
UNCRACKABLE? The Collatz Conjecture - Numberphile
Hester Graves - The abc conjecture implies that there are only finitely many s-Cullen numbers
introduce abc conjecture
Cameron L. Stewart: A refinement of the abc conjecture
The abc conjecture | Conjecture and the overview of the proof by Shinichi Mochizuki
IMPRESSIVE! Two Students Debunk a Widely Accepted Math Conjecture
Undergraduate math talk: The abc conjecture
An introduction to the abc conjecture - Héctor Pastén Vásquez
abc formodningen abc conjecture
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Can ChatGPT prove a number theory conjecture??
The graph of 'abc conjecture'
Комментарии
 0:06:44
0:06:44
 0:17:42
0:17:42
 0:08:52
0:08:52
 0:07:03
0:07:03
 0:00:40
0:00:40
 0:00:58
0:00:58
 0:14:25
0:14:25
 0:01:10
0:01:10
 0:09:12
0:09:12
 0:28:16
0:28:16
 0:03:42
0:03:42
 0:01:33
0:01:33
 0:07:52
0:07:52
 0:15:33
0:15:33
 0:23:30
0:23:30
 0:33:22
0:33:22
 0:03:00
0:03:00
 0:04:55
0:04:55
 0:21:29
0:21:29
 0:53:44
0:53:44
 0:01:38
0:01:38
 0:00:38
0:00:38
 0:00:28
0:00:28
 0:00:54
0:00:54