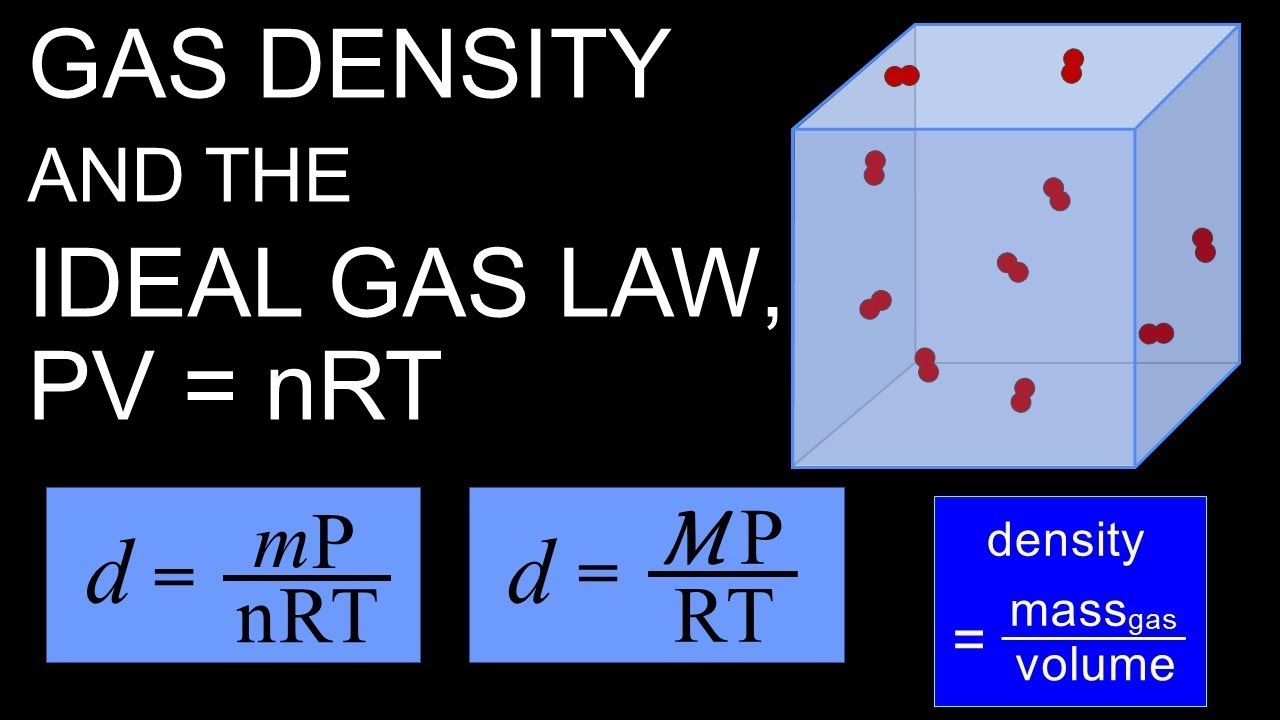
Gas density and PV=nRT, the ideal gas law

What is gas density and how does it fit mathematically into PV=nRT? Also included are two practice problems using d=mP/nRT and d=MP/RT including molar mass and identifying the gas.

CC Academy videos are easy 101 crash course tutorials for step by step Chemistry help on your chemistry homework, problems, and experiments.

- Solution Stoichiometry Tutorial: How to use Molarity
- Stoichiometry
- Quantum Numbers
- Rutherford's Gold Foil Experiment, Explained
- Covalent Bonding Tutorial: Covalent vs. Ionic bonds
- Metallic Bonding and Metallic Properties Explained: Electron Sea Model
- Effective Nuclear Charge, Shielding, and Periodic Properties
- Electron Configuration Tutorial + How to Derive Configurations from Periodic Table
- Orbitals, the Basics: Atomic Orbital Tutorial — probability, shapes, energy
- Metric Prefix Conversions Tutorial
- Gas Law Practice Problems: Boyle's Law, Charles Law, Gay Lussac's, Combined Gas Law
- Ionic Bonds and Compounds
- Chemical reaction types
- product prediction for specific reaction types
- Surface Tension
- what is heat
- what is fire
- The Bohr Model of the Atom
- Organic Molecules and the Versatility of Carbon
- Hybrid Orbitals-- Valence Bond Theory
- Ideal Gas Law and Gas Density

--More on gas density--Wikipedia July 2019--
The density, or more precisely, the volumetric mass density, of a substance is its mass per unit volume. The symbol most often used for density is ρ (the lower case Greek letter rho), although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume: ρ = m/V
where ρ is the density, m is the mass, and V is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume,[2] although this is scientifically inaccurate – this quantity is more specifically called specific weight.

For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure but certain chemical compounds may be denser.

To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative density" or "specific gravity", i.e. the ratio of the density of the material to that of a standard material, usually water. Thus a relative density less than one means that the substance floats in water.

The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Increasing the pressure on an object decreases the volume of the object and thus increases its density. Increasing the temperature of a substance (with a few exceptions) decreases its density by increasing its volume. In most materials, heating the bottom of a fluid results in convection of the heat from the bottom to the top, due to the decrease in the density of the heated fluid. This causes it to rise relative to more dense unheated material.

The reciprocal of the density of a substance is occasionally called its specific volume, a term sometimes used in thermodynamics. Density is an intensive property in that increasing the amount of a substance does not increase its density; rather it increases its mass.

An ideal gas is a theoretical gas composed of many randomly moving point particles whose only interactions are perfectly elastic collisions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.

In most usual conditions (for instance at standard temperature and pressure), most real gases behave qualitatively like an ideal gas. Many gases such as nitrogen, oxygen, hydrogen, noble gases, and some heavier gases like carbon dioxide can be treated like ideal gases within reasonable tolerances.[1] Generally, a gas behaves more like an ideal gas at higher temperature and lower pressure,[1] as the potential energy due to intermolecular forces becomes less significant compared with the particles' kinetic energy, and the size of the molecules becomes less significant compared to the empty space between them. One mole of an ideal gas has a volume of 22.710947(13) litres[2] at standard temperature and pressure (a temperature of 273.15 K and an absolute pressure of exactly 105 Pa) as defined by IUPAC since 1982.
WIKIPEDIA Jan 18 2019

[aarishhanif]

Finally, someone talks about the relationships of density. Thanks!

[adnonalumbert]

LUV this vid, and seems to be filling a gap on youtube. Perfectly done, perfectly explained. THANKS!

[bubbahotep]

Another great video. You have a really great channel.

[smartscience]

Hola!!! I am twelve years and i am admired by your lesson much but which class we'll gonna take the lesson☺

[uveselic]

Excellent! May I ask which "blackboard" software do you use for explanations. Looking for suggestions for me for my students

[pauldolinko]

great explanation!! Thanks!!!. Luv yer channell!!!!

[marigeo]

@3:14 how the value for R differed based on wether the pressure was measured in atm vs. kPa, how can we convert between units of measurement? In other words, how did you know that “under these conditions, the pressure would be 101.3 kPa”?
Or better, what can I search on YouTube to find videos explaining this?

To add on to this: If you’re given the values for R, V, T, and n, which give you a value of 101.3 for P, but you don’t know the unit of measurement, how do you know it’s kPa rather than atm?

[smartscience]

Hi again, we'll gonna take this lesson in grade 10 or 11 or 12 or college?

[হিরোআলম-ণ৮ভ]

Sir, you are too great . Could you please recommend me a good CHEMISTRY textbook for HiGhScHOoL

[Sunita-cxvb]

Si unit of density is kg/m³ by MP/RT how plzz tell