filmov
tv
Area of polygons, including in a grid

Показать описание
The basic principle for calculating the area of polygons, such as pentagons, hexagons, heptagons, and so on, is to divide the polygon into triangles (or other simple shapes), figure out the areas of those, and add them.
We do that for one quadrilateral. Then I show another method which works well for polygons in the coordinate grid. You draw a rectangle AROUND the polygon. Then you figure out the areas of the right triangles that are between the actual polygon and the surrounding rectangle, and subtract the areas of those from the area of the rectangle.
Lastly in this lesson we calculate the area of a trapezoid... not by using the formula, but by dividing it into two triangles and a rectangle. Nothing difficult there, but the main point we learn that it is SO very IMPORTANT to keep track of and record your intermediate calculations. :)
This geometry lesson is intended for 6th grade math.
Check out also my geometry worktext -- available both as a digital download and a printed copy:
We do that for one quadrilateral. Then I show another method which works well for polygons in the coordinate grid. You draw a rectangle AROUND the polygon. Then you figure out the areas of the right triangles that are between the actual polygon and the surrounding rectangle, and subtract the areas of those from the area of the rectangle.
Lastly in this lesson we calculate the area of a trapezoid... not by using the formula, but by dividing it into two triangles and a rectangle. Nothing difficult there, but the main point we learn that it is SO very IMPORTANT to keep track of and record your intermediate calculations. :)
This geometry lesson is intended for 6th grade math.
Check out also my geometry worktext -- available both as a digital download and a printed copy:
Area of polygons, including in a grid
How to Calculate the Area of Polygons
Math Antics - Area
Area of Regular Polygons - Hexagons, Pentagons, & Equilateral Triangles With Inscribed Circles
Finding the Area of Arbitrary Polygons With Geometric Algebra
Find Area of Regular Polygon Given Apothem
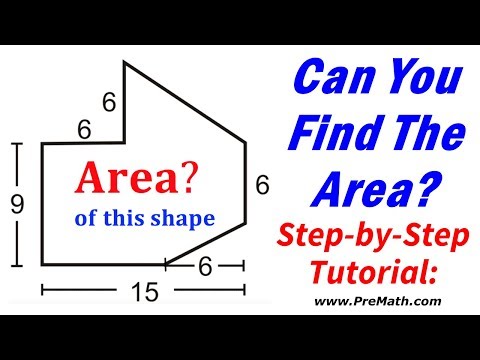
Ex: Find the Area of an L-Shaped Polygon Involving Whole Numbers
Finding the Area of a Composite Figure | Area of Composite Rectangles
Polygons Flat 3-in-1 Measuring Spoons - 2 Spoons with 6 Different Sizes, #amazon
Find the Area of Regular Polygon Given Radius
How to Compute the Area Of Irregular Shapes or Polygons
How to Find the Area of an Irregular Polygon: Step-by-Step Tutorial
Area of polygons
Area of Different Shapes including Regular Polygons
polygons different shapes and their formula area perimeter measurements of angles #maths #polygon
How to find the areas of irregular shapes (including Pick's formula)
Sum of Interior Angles of Any Polygon | SAT and ACT Prep | Math
Find the area of polygons by decomposing into triangles, rectangles, parallelograms, and trapezoids
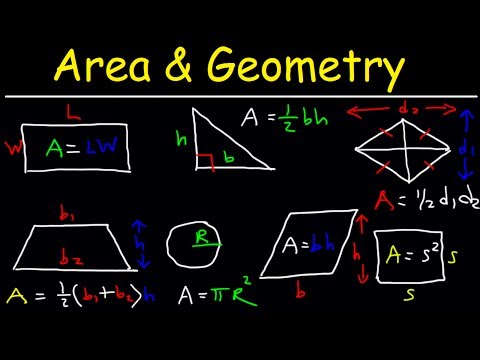
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Use only 1 formula to find the area of this polygon 🧐|higher-order thinking|#Shorts
Maths shorts & Tricks. Polygon names 👍
Finding the Area of Composite Figures with Triangles | Math with Mr. J
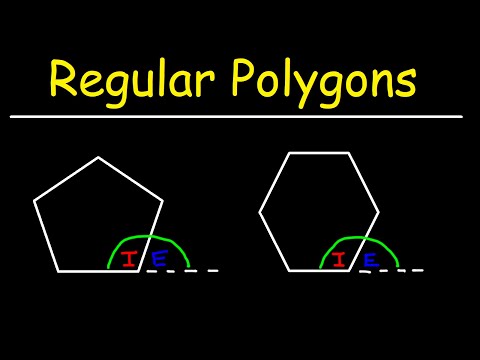
How To Calculate The Interior Angles and Exterior Angles of a Regular Polygon
About polygons//sides,angles, diagonals👈👈✅✅
Комментарии
 0:10:17
0:10:17
 0:06:55
0:06:55
 0:10:26
0:10:26
 0:23:35
0:23:35
 0:00:52
0:00:52
 0:02:36
0:02:36
 0:03:20
0:03:20
 0:07:14
0:07:14
 0:00:44
0:00:44
 0:02:46
0:02:46
 0:00:23
0:00:23
 0:05:38
0:05:38
 0:00:05
0:00:05
 0:14:30
0:14:30
 0:00:06
0:00:06
 0:09:22
0:09:22
 0:00:33
0:00:33
 0:05:33
0:05:33
 0:20:35
0:20:35
 0:01:00
0:01:00
 0:00:18
0:00:18
 0:06:03
0:06:03
 0:13:13
0:13:13
 0:00:08
0:00:08