filmov
tv
Find all Integer Solutions

Показать описание
We find all combinations of 40 integers whose sum and product are both 40.
00:00 Intro
00:15 Making a start
02:18 Ruling out some cases
05:17 Finding solutions
00:00 Intro
00:15 Making a start
02:18 Ruling out some cases
05:17 Finding solutions
Find All Integer Solutions | Number Theory | Math Olympiad Training
Find all Integer Solutions
Find all integer solutions (Russian Math Olympiad)
Find All the Integer Solutions | Use This Tricks
Can You Find Integer Solutions? | Diophantine Equations | Math Olympiad Training
Find all Integer Solutions
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
Math Olympiad Problem | Finding all integer solutions | You should be able to solve this
Can You Solve This Diophantine Equation from Romanian Math Olympiad?
This question looks impossibly hard at first. But work carefully and the solution is beautiful.
Find all Integer Solutions - A Modular Arithmetic Trick
Can you find all the Integer solutions?
Can you find all integer solutions here? | HOW TO SOLVE | Algebra
Italy - Math Olympiad Problem | Find all integer solutions
Find all integer solutions of the equation x^3+y^3+z^3=3xyz.
Are There Any Integer Solutions?
All Integer Solutions to the Diophantine Equation? | Perfect Squares | Pythagorean | Math Olympiad
Math Olympiad Problem | Finding all integer solutions involving square roots | Modification from BMO
Finding ALL Integer Solutions to a^b = b^a
Find all Positive Integer Solutions
Find all integer solutions of the equation x^2-4yz=115.
Complete the Product to find all integer solutions of xy - 3x + 2y = 0
Finding all solutions to a linear Diophantine equation
A Diophantine Equation | Find Positive Integer Solutions
Комментарии
 0:02:23
0:02:23
 0:19:55
0:19:55
 0:20:56
0:20:56
 0:03:50
0:03:50
 0:01:54
0:01:54
 0:10:06
0:10:06
 0:07:40
0:07:40
 0:05:45
0:05:45
 0:06:34
0:06:34
 0:08:25
0:08:25
 0:10:46
0:10:46
 0:04:52
0:04:52
 0:15:03
0:15:03
 0:07:19
0:07:19
 0:08:07
0:08:07
 0:07:27
0:07:27
 0:03:52
0:03:52
 0:04:26
0:04:26
 0:12:58
0:12:58
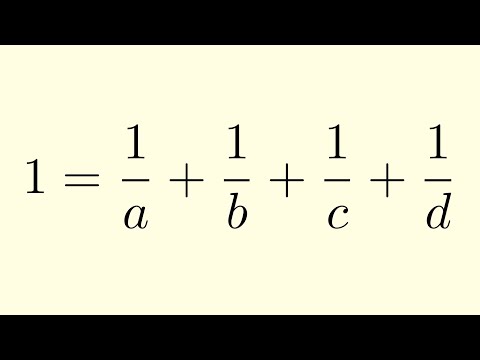 0:11:17
0:11:17
 0:03:25
0:03:25
 0:05:49
0:05:49
 0:04:37
0:04:37
 0:06:11
0:06:11