filmov
tv
Find all Positive Integer Solutions
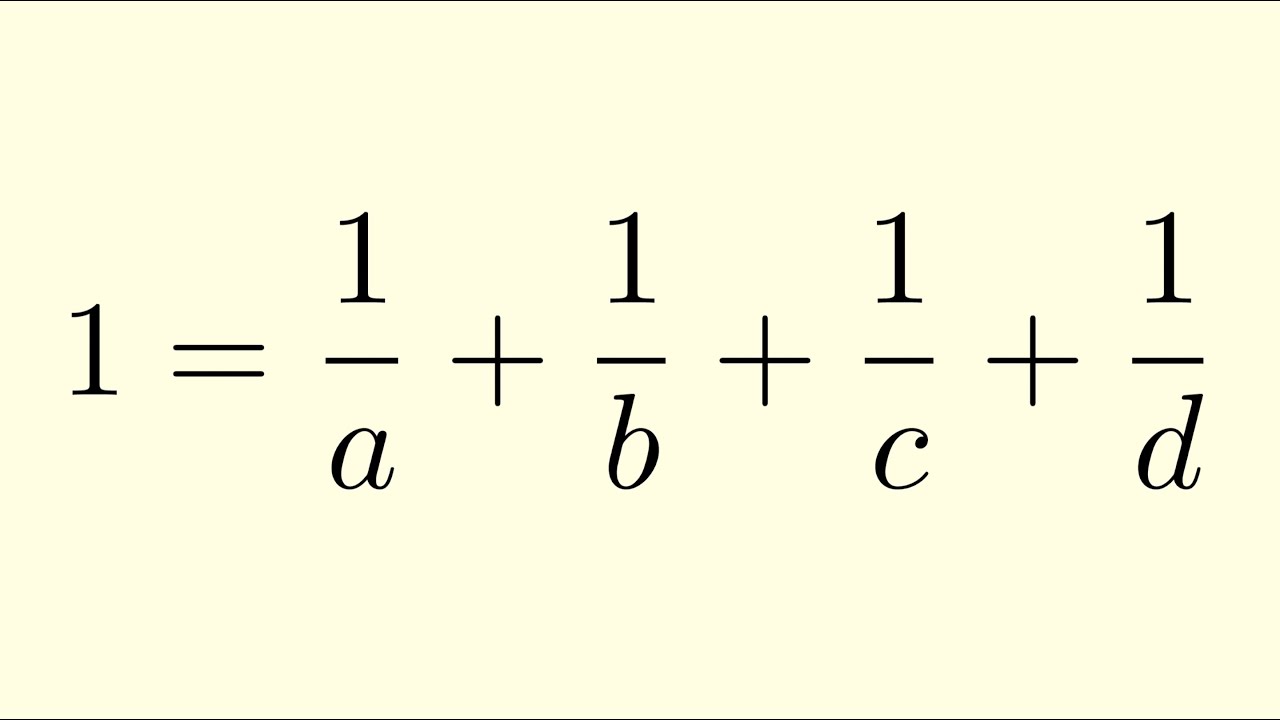
Показать описание
We find all ways of expressing 1 as a sum of 4 distinct (positive) unit fractions.
00:00 Intro
00:10 Values of a
02:09 Values of b
04:38 Values of c
07:01 Finding solutions
00:00 Intro
00:10 Values of a
02:09 Values of b
04:38 Values of c
07:01 Finding solutions
Find all Positive Integer Solutions
Find All the Integer Solutions | Use This Tricks
Find all Integer Solutions
Find all Integer Solutions
Solve the Rational Equation for positive integer solutions.
Can you find positive integer solution for x and y from ONE equation? | Olympiad Math
Are There Any Integer Solutions?
Find all positive integer solutions (n+21)/10 = ⌊√n⌋
MATR1544 10/05/24 |Minimum U Maximum Values |Intervals of Increasing U Decreasing| Concave Up U Down
Find all positive integer solutions to floor(x/9) = floor(x/11); Black Book, Function Problem 54
Beautiful Equation | All Positive Integer Solutions #maths
Find all integer solutions (Russian Math Olympiad)
Find positive integer solutions: 1/x + 1/y = 1/5
Number of Positive Integer Solutions How to Find Part 2
Math Olympiad Problem | Use this TRICK, No Fumbling! | Find all the Integer Solutions
A Diophantine Equation | Find Positive Integer Solutions
Number of Non-Negative Integer solutions of the equation x + y + z = 10 | General Case Explained
Find All Integer Solutions | Number Theory | Math Olympiad Training
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
Find all integer solutions of the equation x^3+y^3+z^3=3xyz.
🔍 Positive Integer Solutions: Solving 11x + 13y = 369 Equation
An Equation With Integer Solutions
Find all positive integer solutions to sqrt(x) + sqrt(y) = sqrt(567) without squaring both sides.
1237. Find Positive Integer Solution for a Given Equation
Комментарии
 0:11:17
0:11:17
 0:03:50
0:03:50
 0:19:55
0:19:55
 0:10:06
0:10:06
 0:04:55
0:04:55
 0:04:55
0:04:55
 0:07:27
0:07:27
 0:06:32
0:06:32
 0:54:27
0:54:27
 0:05:31
0:05:31
 0:04:22
0:04:22
 0:20:56
0:20:56
 0:05:59
0:05:59
 0:03:27
0:03:27
 0:12:28
0:12:28
 0:06:11
0:06:11
 0:09:41
0:09:41
 0:02:23
0:02:23
 0:07:40
0:07:40
 0:08:07
0:08:07
 0:01:29
0:01:29
 0:08:40
0:08:40
 0:07:59
0:07:59
 0:01:31
0:01:31