filmov
tv
Verify the Trigonometric Identity (sec(theta) - 1)(sec(theta) + 1) = tan^2(theta)

Показать описание
Verify the Trigonometric Identity (sec(theta) - 1)(sec(theta) + 1) = tan^2(theta)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus Integration Insanity
Differential Equations Course
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus Integration Insanity
Differential Equations Course
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Verify the Trigonometric Identity sin(theta)(cot(theta) + tan(theta)) = sec(theta)
Verify the Trigonometric Identity (sec(theta) - 1)(sec(theta) + 1) = tan^2(theta)
Verify the Trigonometric Identity sin^2(theta)/cos(theta) = sec(theta) - cos(theta)
Verifying a trigonometric Identities
tan(theta)*sin(theta) + cos(theta) = sec(theta), verify the identity
(sec theta - 1) / (1 - cos theta) = sec theta, verify the identity
tan^2(theta) / sec(theta) = sec(theta) * tan(theta), verify the identity
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
Class 10 Maths | Exercise 8.3 Question 4 (iii) | Trigonometry NCERT Solutions made easy
sec(theta)cot(theta) = csc(theta), prove the identity
Verify the Identity sin(theta)(tan(theta)+cot(theta))=sec(theta), Write in Terms of Sine and Cosine
Verify tan theta + cot theta = sec theta csc theta
cot θ ∙ sec θ = csc θ Verify the identity. Show your work
Prove this Trigonometric Identity | Step-by-Step Explanation
VERIFY/PROVE TRIGONOMETRIC IDENTITY
2020 Maths Advanced HSC Q19 Prove the trigonometric identity sec(θ)-cos(θ)=sin(θ)tan(θ)
Verifying a simple trigonometric identity
Verify sin theta (cot theta + tan theta) = sec theta
Verify trigonometric identities | Q16 P2 | 11A | EoT2 |
Verify sec theta - csc theta = (sin theta - cos theta)/(sin theta cos theta)
Trigonometry Class 10 | Trigonometry Identities| Trigonometry Formulas #fun #shorts #youtubeshorts
Trig Identities
Sec 5.2: Verifying Trigonometric Identities
Prove the trig identity: 1+tan^2 = sec^2
Комментарии
 0:06:56
0:06:56
 0:02:46
0:02:46
 0:01:17
0:01:17
 0:05:12
0:05:12
 0:00:50
0:00:50
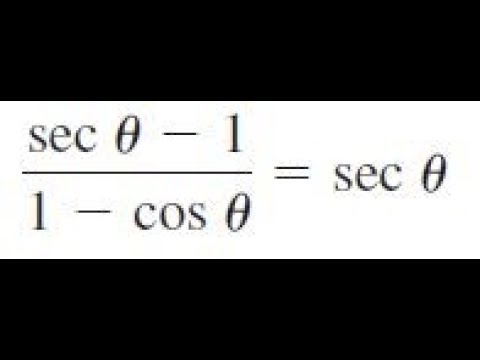 0:02:22
0:02:22
 0:00:52
0:00:52
 0:04:15
0:04:15
 0:07:49
0:07:49
 0:00:44
0:00:44
 0:04:52
0:04:52
 0:01:06
0:01:06
 0:00:45
0:00:45
 0:07:23
0:07:23
 0:07:22
0:07:22
 0:01:33
0:01:33
 0:00:58
0:00:58
 0:01:11
0:01:11
 0:11:17
0:11:17
 0:00:48
0:00:48
 0:00:14
0:00:14
 0:27:57
0:27:57
 0:10:53
0:10:53
 0:02:54
0:02:54