Continued Fractions 1: Introduction and Basic Examples - LearnMathsFree

Показать описание

---

This is the first part in a video series about continued fractions. In this video, we define a finite continued fraction and explore some basic examples. More to follow.

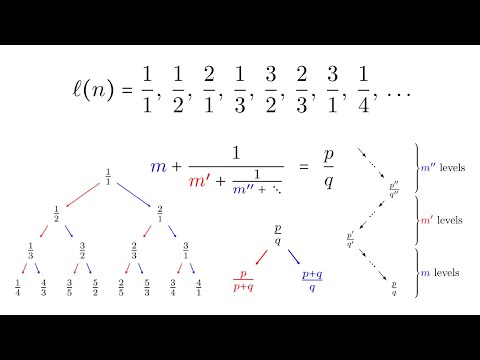
Continued fractions are believed to have first appeared around 300 BC, in Euclid's Elements. A continued fraction is a sequence of integers arranged in a "nested fraction" format: that is, it is an expression obtained by writing a number as the sum of a number plus the reciprocal of another number, then writing *that* number as a number plus the reciprocal of another number, and so on. In this way, one obtains a sequence of numbers, written [a_0, a_1, ..., a_n] in the case of a finite continued fraction (which converges to some rational number), or [a_0, a_1, ... ] in the case of an infinite continued fraction (which can converge to any real number).

The aim of this series is to apply continued fractions in a number of contexts, most notably, to the solution of Pell's equation, x^2 - dy^2 = 1 (where d is square-free), and as a corollary, to solve equations of the form x^2 + dy^2 = k, where d may be positive or negative.

Рекомендации по теме

Комментарии

Thanks heaps CrystalMath! This video is awesome and really easy to understand. My friends and i have a maths assignment with a heavy focus on continued fractions and this video has helped us all a lot! Its great to see people with a passion for maths posting on youtube. We are all really grateful for this video especially. Keep up the good work!!!

danielpetersen

This is the best explanation of continued fractions I’ve ever come across! Why is that some mathematicians feel the need to make everything so complicated or are they poor at communication or even worse maybe they suffer from high priest syndrome where they don’t want to properly share their knowledge with ordinary folk?

frankwood

I'd come across a few videos on continued fractions before, but I think this was the coolest one. I'd also never seen someone go the other way and construct a continued fraction before!

PunmasterSTP

Nice intro!

One remark, FWIW:
The semicolon after the first term, isn't necessary, but I think it's a good idea, because it makes clear that "this is the integer part, " so that when you deal with a fraction < 1, you can omit the "0."

This does require agreement that when the bracketed form is written and there's no semicolon, that it's starting right in on the fractional part; that the integer part = 0.

I'm now proceeding to Part 2, where I'm keen to see how you treat the Pell's Equation solution method, using CF.
I developed a means of doing that on my own a few decades ago, and later found that it closely matched an established method, but I'm curious to see whether there might be anything new that I haven't already encountered.

ffggddss