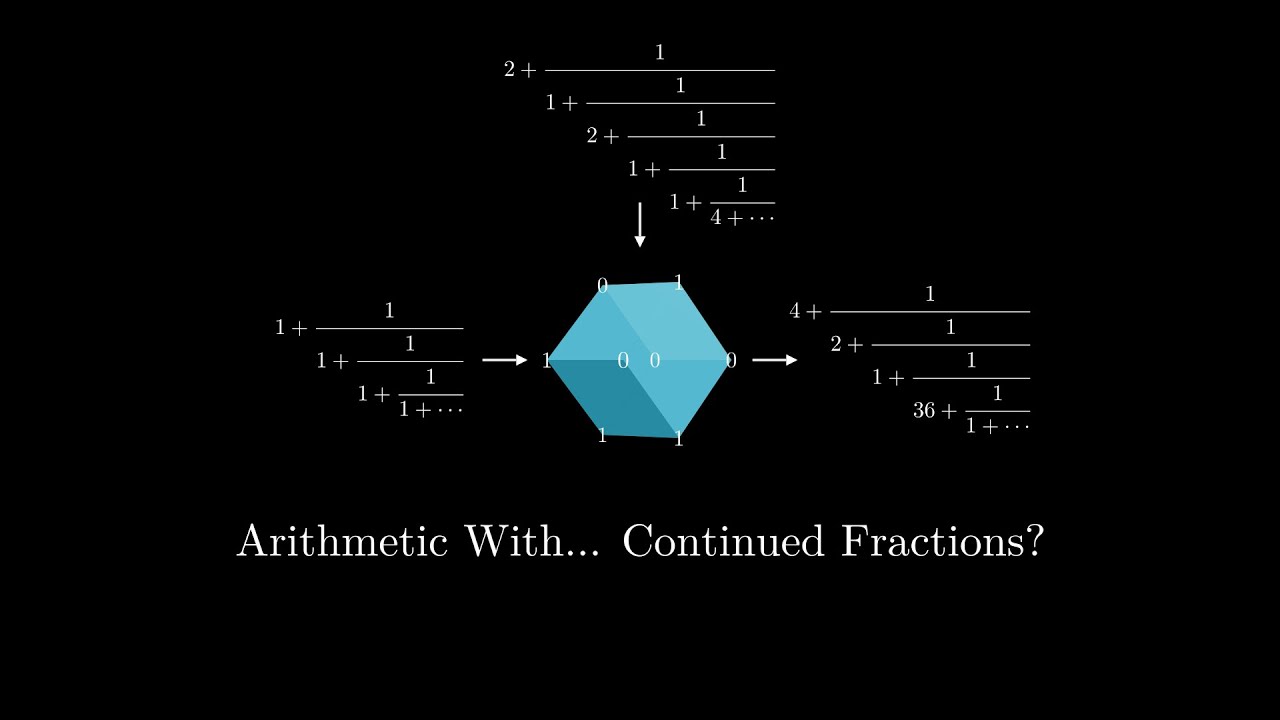
Arithmetic With... Continued Fractions?? #SoME2

Arithmetic! On continued fractions! It's possible, but not well known or widely used in practice. This video explores the basics of this underappreciated area of math.

SOURCES & FURTHER READING:

Continued Fraction Arithmetic (1977)
Speculatively Redundant Continued Logarithm Representation (2010)
Finite Precision Number Systems Arithmetic (2010)
CONTINUED FRACTIONS FOR HIGH-SPEED AND HIGH-ACCURACY COMPUTER ARITHMETIC (1983)
Hardware Implementation of Continued Logarithm Arithmetic (2006)
Exact Arithmetic on the Stern-Brocot Tree (2003)
Continued Logarithms And Associated Continued Fractions (2016)
Generalized Continued Logarithms and Related Continued Fractions (2017)
High-Precision Arithmetic and Mathematical Physics (2015)

[identityelement]

Its really refreshing, not really understanding a 20 min long math video on yt :)

[chennebicken]

I got really lost even in the first few minutes. I know, that I‘m not the measure of everything, but I would suggest to you explaining more what every step means and what you want to do, so one can follow.
So 1. More talking about the words and mathematical entities, you throw in.
2. Maybe a structure with a few headlines. Something like „And now let‘s explore how we can do arithmetic an them“.

To be concrete: I understand matrix multiplication. But just having an x and a y out of nowhere and transforming it in an unexplained way and then claiming this corresponds to a matrix multiplication? A Natural thing to ask is „What are we doing he, what do we want to achieve?“ If the answer is „Determining the actual fraction from the continued-fraction-represantation.“, then I‘m quite happy, that I got, what you were saying. But I can‘t just assume, what‘s happening next. So (not so Pro-)tip: Please guide us through the topic and through the video and just say it out loud, what you are doing and especially, why you are doing it. That can be 1 or 2 short sentences for every „Scene“.
I Hope, you had fun, creating this content, and I hope, I could help by telling the thinks that help me follow along.

[tonyallen]

I understand just a fraction of a fraction of a fraction of a fraction of a fraction of this.

[mostly_mental]

This is really cool. I'd never seen continued logarithms before, but they seem like a powerful tool.

[xj]

I love dense videos, I paused and proved 11 times through the video.

[plesleron]

Very interesting subject! I ended up a little lost on the ingest/egest formulas and their relationship with matrix multiplication and it's currently 3AM so I'll try giving this another watch when I'm a bit more awake. Otherwise, I think that you spoke very clearly in spite of the mic quality which I greatly appreciate.

I'm looking forward to more videos!

[maxreenoch]

Is this Bill Gosper the same guy who discovered the Gosper glider gun in Game of Life?

[lame_lexem]

yeah.. i should revise this later (you lost me when cube appeared), definitely a good video!

[tricanico]

This is an awesome topic! Thanks for sharing.
However I must say, the video feels rushed.
I know about continued fractions and still you managed to lose me very quickly. Can't imagine how it's like for those who didn't know about them.
You use terms you don't define like it's nothing.

I must say again, great topic and thanks for sharing. And it's never too late for a second edition! haha. Cheers!

[fuuryuuSKK]

the "only three bits to specify a term" made me think about how one might use a Huffman tree to encode the number using on average even less bits:

If the tree is maximally unbalanced, the biggest codepoints of a set of eight would have length 7 (example codepoints might be 0, 10, 110, 1110, 11110, As such, we can represent the tree using just three bits for the length of each codepoint, with the tree structure being implicit since it doesn't actually matter *which* codepoint is used to represent an element, so we can just go through the at most 7x3=21 bits (since the last codepoint length is redundant too, seeing as the tree only has the one remaning spot at most, which is left over for the eighth element to fill with it's codepoint. Similarly, if you have filled the tree using any subset of the set of the first six elements, you can omit the subsequent zeroes.), and if we have the element present at all (meaning the codepoint has length >0), assign the smallest available codepoint to the respective element. Thus, if we have a very long representation, we would be able to store that representation far more densely, with a bit of added overhead for the decryption.

This all hinges on the fact that usually, you would likely not have all eight symbols be part of your representation, or at least not all in approximately equal amounts, and thus would benefit from the space-saving properties of Huffman encoding. If however you do have a number that would not save the 22 bits necessary to offset the space the "tree" list of seven bit triplets occupies and gain space, you *can* just save it unencoded.

I do recognize that this almost entirely missed the point of the video, but the video itself assumes prior knowledge on the specific field of continued fractions, which I mostly lack.

[tejing]

I was aware that you could compute with continued fractions representations through an injest/ejest approach like this, but I had never encountered the continued logarithms. I'm going to have to play with those a bit.

One suggestion: Keep more data on the screen at a time, especially when you're demonstrating something. The sequence at 12:04, for example, would be much easier to understand if the entire sequence was displayed at once, so you could refer back to previous values and compare to understand what's happening.

[canaDavid]

This is very cool!
One thing i might have missed, how would one convert these [continued logarithms] to binary and/or decimal, to output?

[TheKivifreak]

Super nice! I think you could implement continued fractions with codata and coinduction in Haskell 🤔

[NUCLEICUS]

Verry interesting work. I just want to know what sotware are you using for animation.
Thank you

[dalembertianblitz]

you wouldnt happen to have a link to a pdf of either the paper by GOSPER or BRABEC would you? The latter seems to be requiring a university log in, but I'd love the opportunity to read them both...

[FareSkwareGamesFSG]

Is there a mistake in the second continued fraction's representation at 2:04?

[elkinmontoya]

Random thought: given the expression for egestion: y=ax+b/cx+d, and also the relationship with matrices and quadratic forms; does this have any relation to automorphic functions?

[animeshjain]

audio could have been way better in otherwise great video

[vector]

I'm all in favor of videos on math, especially in this age of obscurantism and publicly acceptable math phobia, but this video does very little to shed light on applications of continued fractions.

All you do is rush through a list of results. Zero motivation, no worked examples.
This kind of video is counterproductive. I suggest you run your videos past friends or associates for constructive criticism before posting.

[becker]

Enjoyable video, but the audio sounds muffled. Potato-quality.