filmov
tv
Finding the Area of a Non-Right Triangle

Показать описание
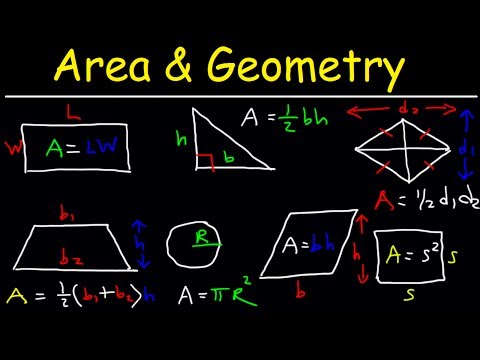
Math Antics - Area
Finding the Area of a Composite Figure | Area of Composite Rectangles
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
How to Find the Area of a Rectangle | Math with Mr. J
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Find the Area Challenge
Area for Kids
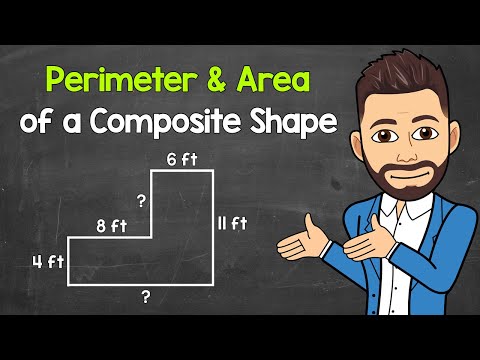
Finding the Perimeter and Area of a Composite Shape | L-Shaped Example | Geometry | Math with Mr. J
Find the Blue Shaded Area
How to Find the Area of a Square | Math with Mr. J
Finding the Area of a Triangle | A Step-By-Step Guide | Math with Mr. J
How to Find the Area of a Circle | Area of a Circle Step by Step
Finding the Area of Composite Figures with Triangles | Math with Mr. J
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Area of a Trapezoid (Trapezium) | Math with Mr. J
Area of Parallelograms | How to Find the Area of a Parallelogram
Area of a Trapezoid | MathHelp.com
Area of a Circle | Beat the Calculator #shorts
Area of a Rectangle - Math for Kids
Finding The Area Under The Curve Using Definite Integrals - Calculus
GCSE Maths - How to Find the Area of Rectangles, Parallelograms, Triangles and Trapeziums #105
How to Find the Area of a Composite Shape | L-Shaped Example | Math with Mr. J
Finding the Area of a Composite Figure
How to Find the Area of Rectangles and Squares | Math with Mr. J
Комментарии
 0:10:26
0:10:26
 0:07:14
0:07:14
 0:22:10
0:22:10
 0:04:43
0:04:43
 0:20:35
0:20:35
 0:04:33
0:04:33
 0:08:58
0:08:58
 0:08:21
0:08:21
 0:02:36
0:02:36
 0:02:48
0:02:48
 0:07:35
0:07:35
 0:06:39
0:06:39
 0:06:03
0:06:03
 0:06:37
0:06:37
 0:06:14
0:06:14
 0:04:30
0:04:30
 0:01:39
0:01:39
 0:00:52
0:00:52
 0:03:06
0:03:06
 0:34:24
0:34:24
 0:05:32
0:05:32
 0:05:21
0:05:21
 0:02:02
0:02:02
 0:06:57
0:06:57