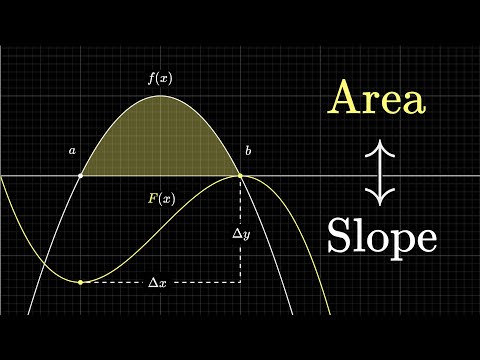
Derivation of the integral of 1/(a^2+x^2)=1/a*arctan(x/a)+C.

You've probably seen the integral of 1/(a^2+x^2) in a standard table of integrals, but how do we derive it?

It turns out we can use a simple u-substitution or informally use the reverse chain rule in order to compute the integral of 1/(a^2+x^2).

In this video, we start by showing the chain rule backwards approach to the integral, then we use a u-substitution to verify that we get the same answer: the integral of 1/(a^2+x^2) is 1/a*arctan(x/a).