filmov
tv
Implicit differentiation and related rates with demand function business calculus

Показать описание
In this calculus example, the demand function for a product is given by p(n)= where p is the price in dollars and n is the quantity in thousands. If adverse weather conditions are driving the price up by $ per week, find the rate at which the demand quantity for the product is changing when the price is $.
We use implicit differentiation and related rates with a demand function to calculate the change in demand dn/dt (sometimes dq/dt) when given rate of change in price dp/dt. Each part of this process is explained and written step-by-step.
We use implicit differentiation and related rates with a demand function to calculate the change in demand dn/dt (sometimes dq/dt) when given rate of change in price dp/dt. Each part of this process is explained and written step-by-step.
 0:08:53
0:08:53
 0:10:32
0:10:32
 0:15:34
0:15:34
 0:18:38
0:18:38
 0:14:34
0:14:34
 0:11:45
0:11:45
 0:25:30
0:25:30
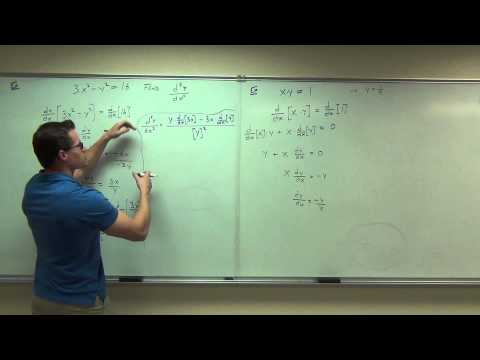 1:08:11
1:08:11
 1:16:11
1:16:11
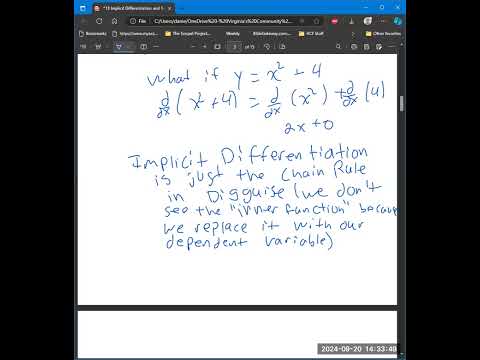 0:38:54
0:38:54
 0:08:29
0:08:29
 0:03:51
0:03:51
 0:13:52
0:13:52
 0:24:53
0:24:53
 0:03:03
0:03:03
 0:46:31
0:46:31
 0:17:36
0:17:36
 0:01:57
0:01:57
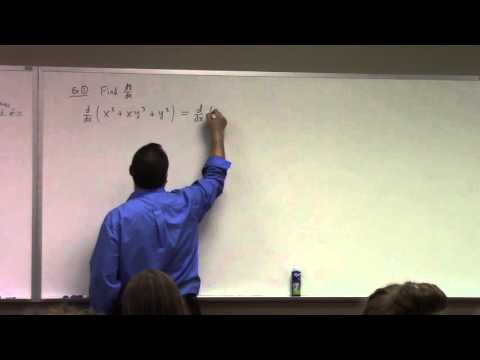 0:59:51
0:59:51
 0:07:55
0:07:55
 0:05:04
0:05:04
 1:45:26
1:45:26
 0:10:03
0:10:03
 0:07:57
0:07:57