filmov
tv
Integrate [sin( x)/ (sin x + cos(x))]

Показать описание
This strategy came by keen observation. It is the first time I ever used it abd I know it works.
Integrate [sin( x)/ (sin x + cos(x))]
Integral of sin(x)
Class 12th – Integral of Sinx/Sin(x-a) | Integrals | Tutorials Point
Solving Integral: ∫ sin x / x dx
Integral of x sin x | #shorts #youtubeshorts #integral #maths
Integral of x*sinx (integration by parts) | Calculus 2 Exercises
Proving a Limit of sin(x)/x
integral of sin(x)/x from 0 to inf by Feynman's Technique
Visualizing the derivative of sin(x)
Integral of e^x sinx
Find the fourier transform of f(x) = 1 if |x| lesser 1 : 0 if |x| greater1. Evaluate ∫(sin x)/x dx
Integrate : ∫ sinx / sin(x - α) dx
How To Solve integration of xSinx by integrating by part 🔥 Integrals of xSinx #maths #integral
Complex Analysis: Integral of sin(x)/x using Contour Integration
Integral 1/sin x
integral of sin(x) from 0 to infinity #math
How to Integrate xsinx^2
Integration of Sin(X) in fx-991es plus Calculator #viral #scientificcalculator
How to integrate x sinx using integration by parts
integrate sin x sin 2x sin 3x dx
Trigonometric Integrals
Fastest way to integrate sinx/x from zero to infty
integral of sin(x^2) haunts me
Integral of sinx cosx
Комментарии
 0:09:05
0:09:05
 0:00:23
0:00:23
 0:02:31
0:02:31
 0:00:56
0:00:56
 0:00:12
0:00:12
 0:03:44
0:03:44
 0:01:00
0:01:00
 0:22:44
0:22:44
 0:00:59
0:00:59
 0:04:56
0:04:56
 0:08:37
0:08:37
 0:07:46
0:07:46
 0:00:54
0:00:54
 0:17:43
0:17:43
 0:00:37
0:00:37
 0:00:19
0:00:19
 0:01:58
0:01:58
 0:00:27
0:00:27
 0:02:52
0:02:52
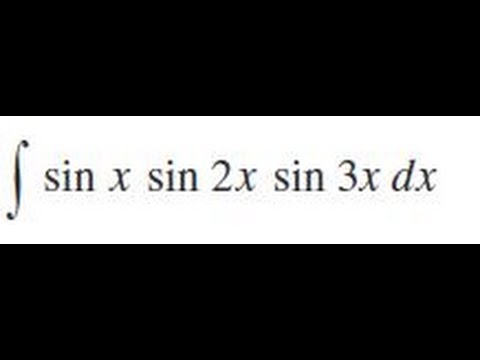 0:01:39
0:01:39
 0:31:29
0:31:29
 0:02:09
0:02:09
 0:00:17
0:00:17
 0:07:09
0:07:09