filmov
tv
A Nice Cubic Equation | Cubic Formula | #PolynomialEquations

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
In this video, I talk about The Cubic Formula in detail.
If you need to post a picture of your solution or idea:
x^3=3x^2-6x+4
#PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
In this video, I talk about The Cubic Formula in detail.
If you need to post a picture of your solution or idea:
x^3=3x^2-6x+4
#PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Nice Cubic Equation
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Simple way to solve a cubic equation
Solving a Nice Cubic System in Two Ways
Solving A Nice Cubic Equation | Math Olympiads
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
A Nice Polynomial Equation | Cubic Formula
so you want to see the cubic formula
Can you Solve this? | Math Olympiad
Determine Cubic Equation grade 12
solving equations but they get increasingly awesome
Solving Simple Cubic Equations
Can you solve this cubic equation by factoring?
GCSE Maths - What are Cubic Graphs & How to Plot Them #78
Factorise Cubic Equation Grade 12: Introduction
Solving a simple cubic equation. A trick you should know!
Determine Cubic Equation grade 12
Determine Cubic Equation grade 12
A Nice Cubic | x^3-3x=2
Using Vieta's Formulas in A Cubic Equation
Solving A Nice Cubic System in Two Ways
How To ACTUALLY Solve a Cubic Equation using Trigonometry
5 simple unsolvable equations
Solving a cubic equation with irrational coefficients. A radical challenge in algebra.
Комментарии
 0:08:34
0:08:34
 0:36:58
0:36:58
 0:04:56
0:04:56
 0:09:13
0:09:13
 0:00:37
0:00:37
 0:10:52
0:10:52
 0:10:56
0:10:56
 0:40:16
0:40:16
 0:08:24
0:08:24
 0:02:58
0:02:58
 0:10:44
0:10:44
 0:09:13
0:09:13
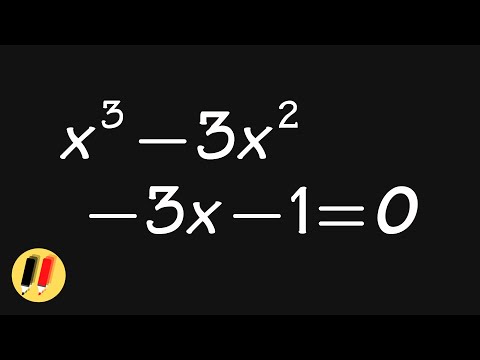 0:00:59
0:00:59
 0:04:50
0:04:50
 0:06:17
0:06:17
 0:06:41
0:06:41
 0:02:54
0:02:54
 0:04:07
0:04:07
 0:08:50
0:08:50
 0:00:33
0:00:33
 0:09:41
0:09:41
 0:14:58
0:14:58
 0:00:50
0:00:50
 0:06:36
0:06:36