filmov
tv
THE BASICS OF FINITE GEOMETRY
Показать описание
THE BASICS OF FINITE GEOMETRY
Note to the viewers: (The following are basics of Finite Geometry but not included in the video:)
Note that the Four Point and Four Line Geometry are almost the same, just the term points and lines differ.
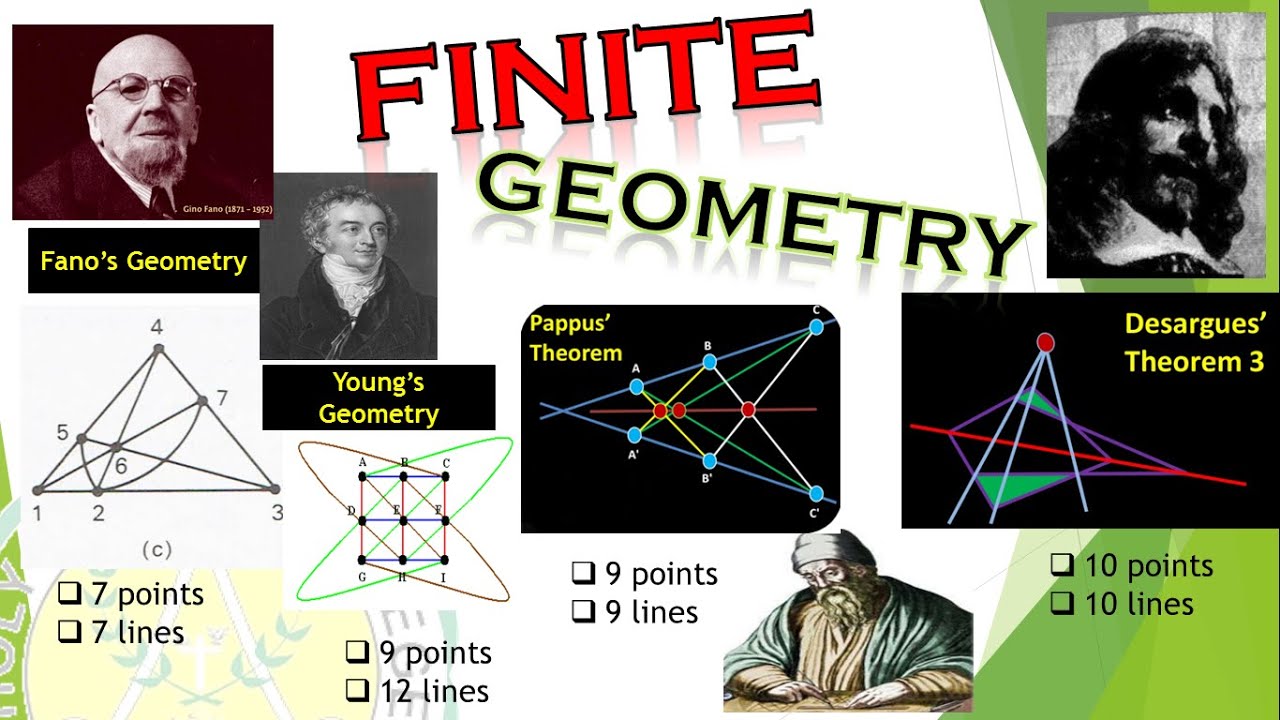
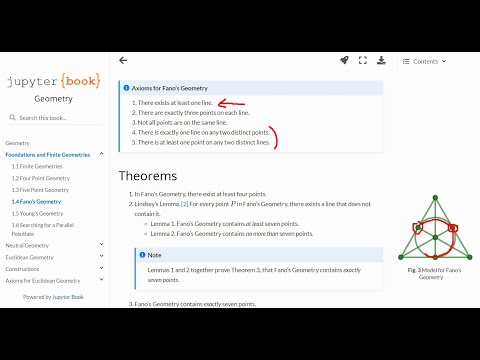
Three Point Geometry
Axioms for the Three Point Geometry:
1. There exist exactly 3 points in this geometry.
2. Two distinct points are on exactly one line.
3. Not all the points of the geometry are on the same line.
4. Two distinct lines are on at least one point.
Theorem 1.1 : Two distinct lines are on exactly one point.
Theorem 1.2 : The three point geometry has exactly three lines.
The Four Line Geometry
The Axioms for the Four Line Geometry:
1. There exist exactly 4 lines.
2. Any two distinct lines have exactly one point on both of them.
3. Each point is on exactly two lines.
Theorem 1.3: The four line geometry has exactly six points.
Theorem 1.4: Each line of the four-line geometry has exactly 3 points on it.
The Four Point Geometry
The Axioms for the Four Point Geometry:
1. There exist exactly 4 points.
2. Any two distinct points have exactly one line on both of them.
3. Each line is on exactly two points.
Theorem 1.5: The four point geometry has exactly six lines.
Theorem 1.6: Each point of the four- point geometry has exactly 3 lines on it.
What is finite Geometry?
Leading figures in Finite Geometry with their configurations:
-Gino Fano
- Young
- Pappus of Alexandria
- Girard Desargues
#Finite Geometry
#Geometry
#Modern Geometry
Note to the viewers: (The following are basics of Finite Geometry but not included in the video:)
Note that the Four Point and Four Line Geometry are almost the same, just the term points and lines differ.
Three Point Geometry
Axioms for the Three Point Geometry:
1. There exist exactly 3 points in this geometry.
2. Two distinct points are on exactly one line.
3. Not all the points of the geometry are on the same line.
4. Two distinct lines are on at least one point.
Theorem 1.1 : Two distinct lines are on exactly one point.
Theorem 1.2 : The three point geometry has exactly three lines.
The Four Line Geometry
The Axioms for the Four Line Geometry:
1. There exist exactly 4 lines.
2. Any two distinct lines have exactly one point on both of them.
3. Each point is on exactly two lines.
Theorem 1.3: The four line geometry has exactly six points.
Theorem 1.4: Each line of the four-line geometry has exactly 3 points on it.
The Four Point Geometry
The Axioms for the Four Point Geometry:
1. There exist exactly 4 points.
2. Any two distinct points have exactly one line on both of them.
3. Each line is on exactly two points.
Theorem 1.5: The four point geometry has exactly six lines.
Theorem 1.6: Each point of the four- point geometry has exactly 3 lines on it.
What is finite Geometry?
Leading figures in Finite Geometry with their configurations:
-Gino Fano
- Young
- Pappus of Alexandria
- Girard Desargues
#Finite Geometry
#Geometry
#Modern Geometry
Комментарии
 0:30:01
0:30:01
 0:48:17
0:48:17
 0:14:05
0:14:05
 0:28:17
0:28:17
 0:30:02
0:30:02
 4:39:37
4:39:37
 0:03:32
0:03:32
 8:43:48
8:43:48
 0:01:36
0:01:36
 1:02:43
1:02:43
 0:53:48
0:53:48
 0:09:11
0:09:11
 0:03:32
0:03:32
 0:14:54
0:14:54
 0:00:59
0:00:59
 0:00:45
0:00:45
 0:01:53
0:01:53
 0:01:57
0:01:57
 0:17:38
0:17:38
 0:49:06
0:49:06
 0:18:26
0:18:26
 0:09:38
0:09:38
 0:01:36
0:01:36
 0:00:50
0:00:50