filmov
tv
Calculus 1, Lecture 3B: Exponential Functions Fundamental Properties (also see the end of Lec 3A)

Показать описание
Start with a visual based on a property from Lecture 3A. Then move on to discussion of more properties of exponential functions. Brief introduction to Mathematica at the end.
(0:00) Visualizing the "addition to multiplication" property of exponential functions.
(3:08) Exponential functions are often written in alternative ways, including using the number e as a base and having a continuous growth rate.
(9:26) Doubling time and half life.
(15:47) Exponential functions are continuous and smooth (differentiable). They have a constant relative rate of change. The domain is the set of all real numbers, and if the initial value is positive, the range is the open interval from 0 to infinity. They are one-to-one. If the codomain is considered to be the set of all positive real numbers, then they are onto. Limiting values.
(26:24) Use Mathematica to solve an exponential function, but the output is not in the most ideal form. I will fix this in Lecture 4A.
(0:00) Visualizing the "addition to multiplication" property of exponential functions.
(3:08) Exponential functions are often written in alternative ways, including using the number e as a base and having a continuous growth rate.
(9:26) Doubling time and half life.
(15:47) Exponential functions are continuous and smooth (differentiable). They have a constant relative rate of change. The domain is the set of all real numbers, and if the initial value is positive, the range is the open interval from 0 to infinity. They are one-to-one. If the codomain is considered to be the set of all positive real numbers, then they are onto. Limiting values.
(26:24) Use Mathematica to solve an exponential function, but the output is not in the most ideal form. I will fix this in Lecture 4A.
 0:31:43
0:31:43
 1:19:27
1:19:27
 0:04:00
0:04:00
 0:39:13
0:39:13
 0:13:23
0:13:23
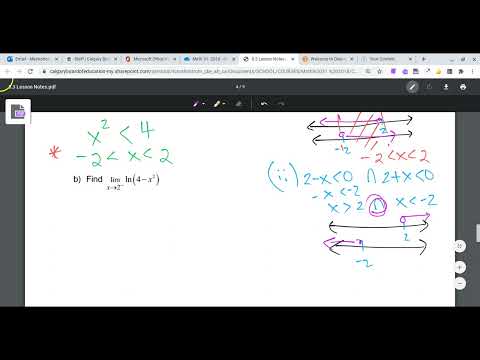 0:10:07
0:10:07
 0:07:03
0:07:03
 0:33:29
0:33:29
 0:13:07
0:13:07
 0:22:20
0:22:20
 0:07:51
0:07:51
 0:23:20
0:23:20
 0:00:13
0:00:13
 0:29:14
0:29:14
 0:38:05
0:38:05
 0:11:52
0:11:52
 0:00:13
0:00:13
 0:15:01
0:15:01
 0:35:29
0:35:29
 0:24:21
0:24:21
 0:15:08
0:15:08
 0:00:12
0:00:12
 0:55:54
0:55:54
 0:23:03
0:23:03