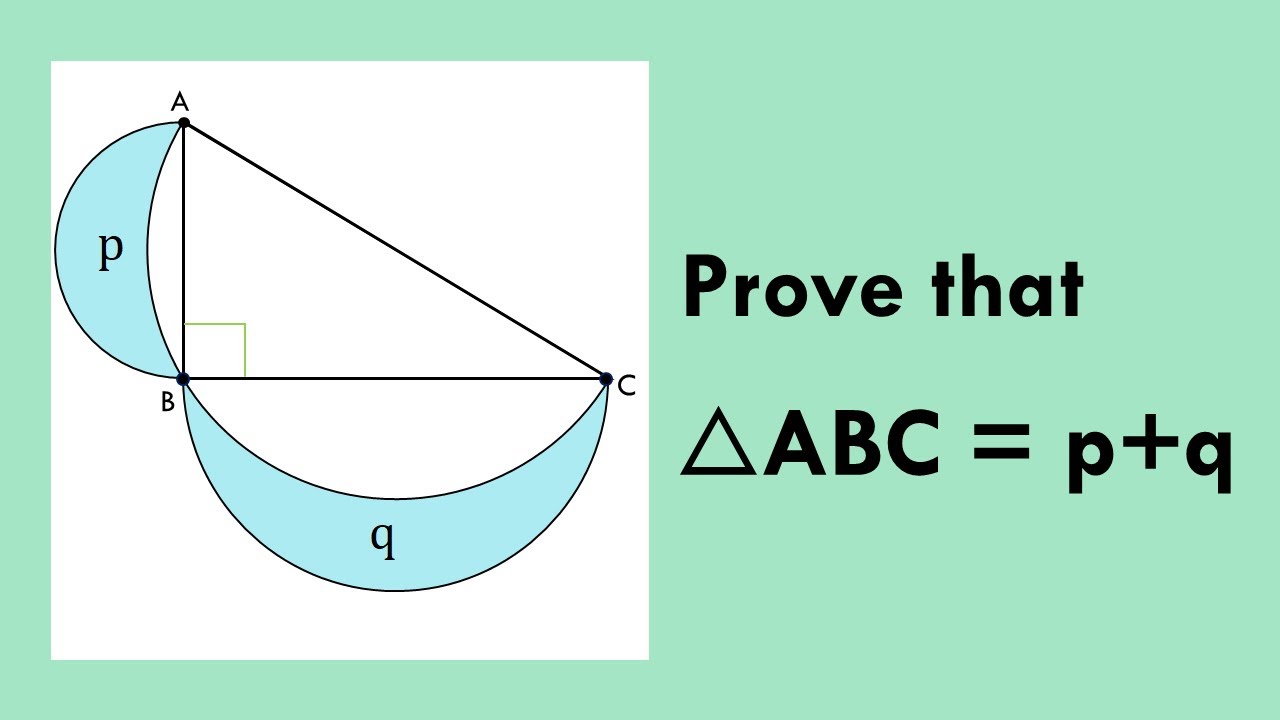
Prove that Area of Triangle ABC is equal to sum of areas of the lunes

Area of the Crescent Shaped | Hippocrates | Fancy Q | Area of the Q

This video presents a very fasinating proving problem in geometry.

The problem presents a right angled triangle with three semicircles on its sides, one on its hypotenuse with hypotenuse as the diameter of the semicircle, one on one of its legs with the length of the leg as the diameter of the semi-circle and another on another leg with the length of the leg as the diameter of another semi circle. The task is to prove that the area of a right angled triangle is equal to the sum of area of lunes formed on its legs. These two lunes standing on the opposite and the adjacent side of the triangles are called Lunes of Alhazen.

This problem is interesting also because, now that the world of Mathematics accepts the fact that squaring the circle is not possible merely with a straightedge and compass, this problem establishes a relation between a triangle and a crescent shaped or moon-shaped circular area.

Anyone with simple understanding of Circle, Diameter, Radius, Circumference, Chord, Segment, Right Angled Triangle, hypotenuse, legs, Pythagorus Theorem etc will very easily be able to solve it.

[rituratnam]

We can see the hard work you put in your videos. Worth a watch!💕

[robertlunderwood]

Most of that stuff you used I was either never taught or forgotten. I carefully labelled the sides of the triangle a, b, and c. The area of the triangle is ab/2. Each of the smaller semicircles have areas of πa^2/4 and πb^2/4. The area of the big semicircle would be πc^2/4, but due to Pythagoras, that is (a^2 + b^2)π/4. The semicircle is divided into three parts: the triangle (ab/2), and a remainder of each of the smaller semicircles once p and q are removed.

Thus, we have πa^2/4 + πb^2/4 = ab/2 + πa^2/4 - p + πb^2/4 - q. We have simple algebra from there.

[mahmoudelboshy]

Good performance
Good luck and keep going on 💯🔥🔥

[abysmalskies]

Like seriously! Nevee thought Pythagorean theorem could be used this way. Go on. Waiting for more !

[carlyet]

Double it up so the area four luns ( p & q luns twice ) plus the area of the disk (diameter hypotuse c) is also two disks (diametres a & b) areas and the rectangle ( a b ).

Diametres :: a b c note a^2 + b^2 = c^2. So a^2 + b^2 - c^2 = 0
Setup:: 2(p+q) + pi/4 . c^2 = pi/4 . a^2 + pi/4 . b^2 + a . b
note :: disk area is pi . r^2 & 2r = d, 4r^2 = d^2 so pi. r^2 = pi/4 . d^2
Simplify:: p + q = 1/2[ a.b + pi/4 ( a^2 + b^2 - c^2 )] = 1/2 . a.b
Area of luns :: p+q. Area of triangle :: 1/2 . a.b

[rakeshsrivastava]

New insights into Pythagoras theorem.Good show.

[pk]

Nice proof . It boils down to the area of the semicircle on the hypotenuse is equal to the sum of the areas of the semicircles on the legs . Then, the semicircle in the demonstration of this fact is flipped 180 degrees ; so, the figure matches the original figure . In effect when the semicircle on the hypotenuse is flipped onto the two semicircle on the legs whose sum of semicircular areas on the legs adds up to the area of the semicircular area on the hypotenuse, we create the two lunes . It is then obvious that the sum of the areas of the lunes is equal to the area of the triangle, I proved the theorem to myself before I watched the video ; but, It took me a great deal of work because I used integral calculus to find the areas of the lunes .

[anusivaNilavu]

❤ 🎉 Lovely work...Looking forward to seeing more solutions like these 🎉 ❤

[sadikshashrestha]

This video makes it easy to understand, and the way you explain is amazing. Keep going dee, all the best.

[amyweeks]

Will it work if the sides of the triangle is not diameters of the semicircle but chords of the semicircle?