filmov
tv
Area of a Circle (equation derived with calculus)

Показать описание
Equation for the area of a circle is derived with integration.
Math Antics - Circles, Circumference And Area
Circles - Area, Circumference, Radius & Diameter Explained!
How to Find the Area of a Circle | Area of a Circle Step by Step
How to Calculate the Circumference of a Circle
Area of a Circle | MathHelp.com
How to find the area of a circle from its equation
What is Area of a Circle? Area Formula & Calculation - [7-5-10]
How to find the center and radius of a circle in standard form
Area of a Circle (equation derived with calculus)
Quick Visual Proof: Area of a Circle
Graphing Circles and Writing Equations of Circles In Standard Form - Conic Sections
How to Calculate the Area of a Circle
How to Find the Area of a Circle | Math with Mr. J
The Area Of A Circle Formula - Simple Intuitive Explanation
Area of a circle
GCSE Maths - How to find the Area and Circumference of a Circle (Circles Part 1) #106
Understanding the Circumference of a Circle Formula
How to write the equation of a circle given the center and area of the circle
Derive the Area of a Circle Using Integration (x^2+y^2=r^2)
Area = πr² Why? Part 1| Fun Math | Don't Memorise
GCSE Maths - Area of a Sector and Length of an Arc of a Circle (Circles Part 3) #108
How to Find the Area of a Circle, Given a Radius or a Diameter
How to find the Area of a Circle #shorts
Kepler’s Impossible Equation
Комментарии
 0:07:56
0:07:56
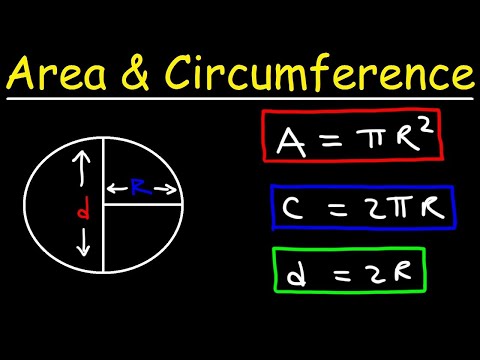 0:17:20
0:17:20
 0:06:39
0:06:39
 0:00:59
0:00:59
 0:01:40
0:01:40
 0:03:55
0:03:55
 0:17:56
0:17:56
 0:05:06
0:05:06
 0:04:49
0:04:49
 0:06:47
0:06:47
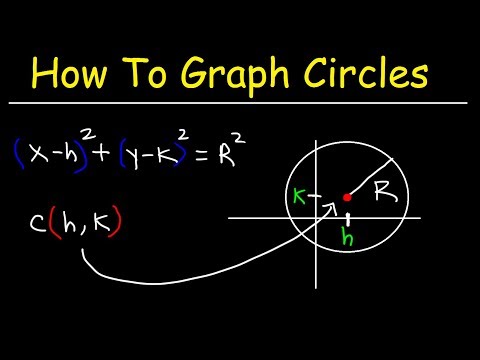 0:10:04
0:10:04
 0:02:27
0:02:27
 0:09:08
0:09:08
 0:01:00
0:01:00
 0:06:45
0:06:45
 0:05:13
0:05:13
 0:00:44
0:00:44
 0:00:53
0:00:53
 0:08:29
0:08:29
 0:01:08
0:01:08
 0:05:39
0:05:39
 0:03:25
0:03:25
 0:00:49
0:00:49
 0:00:51
0:00:51