filmov
tv
Proving the Change of Base Formula for Logarithms #shorts

Показать описание
Thank you for watching my video! Please consider subscribing and sharing my content!
Change of base formula proof | Logarithms | Algebra II | Khan Academy
Proof of the change of base formula
Proving 'Change of Base' Rule
Change of Base Formula - Logarithms
Proving the Change of Base Formula for Logarithms #shorts
Logarithms Review: (2 of 4: Proving the Change of Base Law)
Algebra Ch 47: Logarithmic Functions (24 of 26) How to Prove: Change the Base?
How to Prove 'The Change of Base Formula' for Logarithms: Easy Step-by-Step Explanation
Proving the Change of Base Formula
Prove: Change of Base Property of Logarithms
Change of base formula | Logarithms | Algebra II | Khan Academy
Logarithms / Change of Base (1 of 2: About Base 10)
Change of Base Logarithms Application to Prove Identity
Change of Base, Logarithm
Derivation logarithm change of base formula, common log to natural log, log change of base examples
Logarithms / Change of Base (2 of 2: Deriving the Law)
Change of base formula proof
How to Use the Change of Base Formula if the Base is a Fraction
Use The Change Of Base Formula To Evaluate Logarithms. No calculator
Logarithm Change of Base Formula & Solving Log Equations - Part 1 - [7]
Changing Between Two Bases | Derivation + Example
Logarithms Change of Base Formula
Logarithms: Change of Base Rule Proof
How to Change the Base of a Logarithm (Precalculus - College Algebra 61)
Комментарии
 0:04:59
0:04:59
 0:01:59
0:01:59
 0:03:18
0:03:18
 0:02:39
0:02:39
 0:00:51
0:00:51
 0:09:39
0:09:39
 0:02:56
0:02:56
 0:05:39
0:05:39
 0:04:29
0:04:29
 0:03:28
0:03:28
 0:07:32
0:07:32
 0:07:32
0:07:32
 0:02:23
0:02:23
 0:07:37
0:07:37
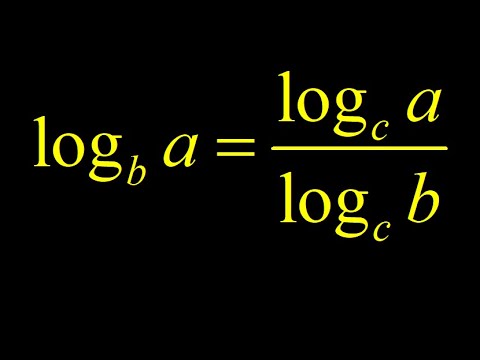 0:03:53
0:03:53
 0:06:40
0:06:40
 0:07:07
0:07:07
 0:01:04
0:01:04
 0:07:07
0:07:07
 0:23:32
0:23:32
 0:07:55
0:07:55
 0:02:05
0:02:05
 0:07:26
0:07:26
 0:09:55
0:09:55