filmov
tv
Deriving EULER's INFINITE SINE PRODUCT using the Mittag-Leffler Pole Expansion of the Cotangent!

Показать описание
Help me create more free content! =)
Sry for the sound problems!
Today we are going to derive a very important number theoretical identity! We are not going to take the heuristic approach euler once did, but rather a more rigorous approach to the whole thing. Let's decompose sine into its linear factors, enjoy! =)
Sry for the sound problems!
Today we are going to derive a very important number theoretical identity! We are not going to take the heuristic approach euler once did, but rather a more rigorous approach to the whole thing. Let's decompose sine into its linear factors, enjoy! =)
Deriving Euler's Infinite Sine Product
Deriving EULER's INFINITE SINE PRODUCT using the Mittag-Leffler Pole Expansion of the Cotangent...
e^(iπ) in 3.14 minutes, using dynamics | DE5
That's right, an infinite product for sin(x) courtesy of Euler (feat. a crazy series for cot(x)...
Euler's infinite pi formula generator
What's so special about Euler's number e? | Chapter 5, Essence of calculus
Infinite product formula for sin(x)
Trigonometric Identities from Euler's Formula
Deriving the Infinite Product Representations for all the Trigonometric Functions!
What is Euler's formula actually saying? | Ep. 4 Lockdown live math
Sine Curve and the Unit Circle
The most beautiful equation in math, explained visually [Euler’s Formula]
If I did this in 1734 I'd be World Famous
Euler Çarpımı - Sine Function 's Euler Product Formula and Proof !
The Basel Problem Part 2: Euler's Proof and the Riemann Hypothesis
ONE NEAT PROOF! Deriving the EULER DEFINITION of the Gamma Function!
Euler's Original Proof Of Basel Problem: Σ(1/n²)=π²/6 — BEST Explanation
Euler's real identity NOT e to the i pi = -1
Derivatives of Exponential Functions
An Interesting Infinite Half-Angle Product Representation for the sin(x)
Every Student Should See This
The Most Beautiful Math Equation...But Why? (with Taylor Series Derivation & a Trig Id Applicati...
Deriving Trig Formulas pg 91
When mathematicians get bored (ep1)
Комментарии
 0:22:47
0:22:47
 0:11:37
0:11:37
 0:04:08
0:04:08
 0:15:36
0:15:36
 0:28:57
0:28:57
 0:13:50
0:13:50
 0:01:18
0:01:18
 0:10:35
0:10:35
 0:15:36
0:15:36
 0:51:16
0:51:16
 0:00:27
0:00:27
 0:26:57
0:26:57
 0:03:57
0:03:57
 0:24:57
0:24:57
 0:58:32
0:58:32
 0:23:28
0:23:28
 0:13:59
0:13:59
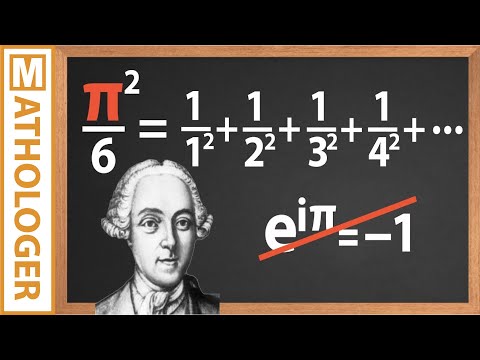 0:17:16
0:17:16
 0:12:03
0:12:03
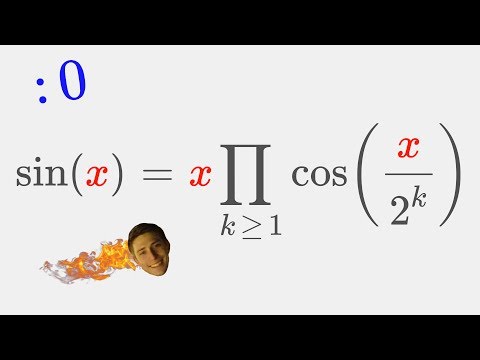 0:10:04
0:10:04
 0:00:58
0:00:58
 0:20:31
0:20:31
 0:15:17
0:15:17
 0:00:37
0:00:37