filmov
tv
Deriving the Infinite Product Representations for all the Trigonometric Functions!
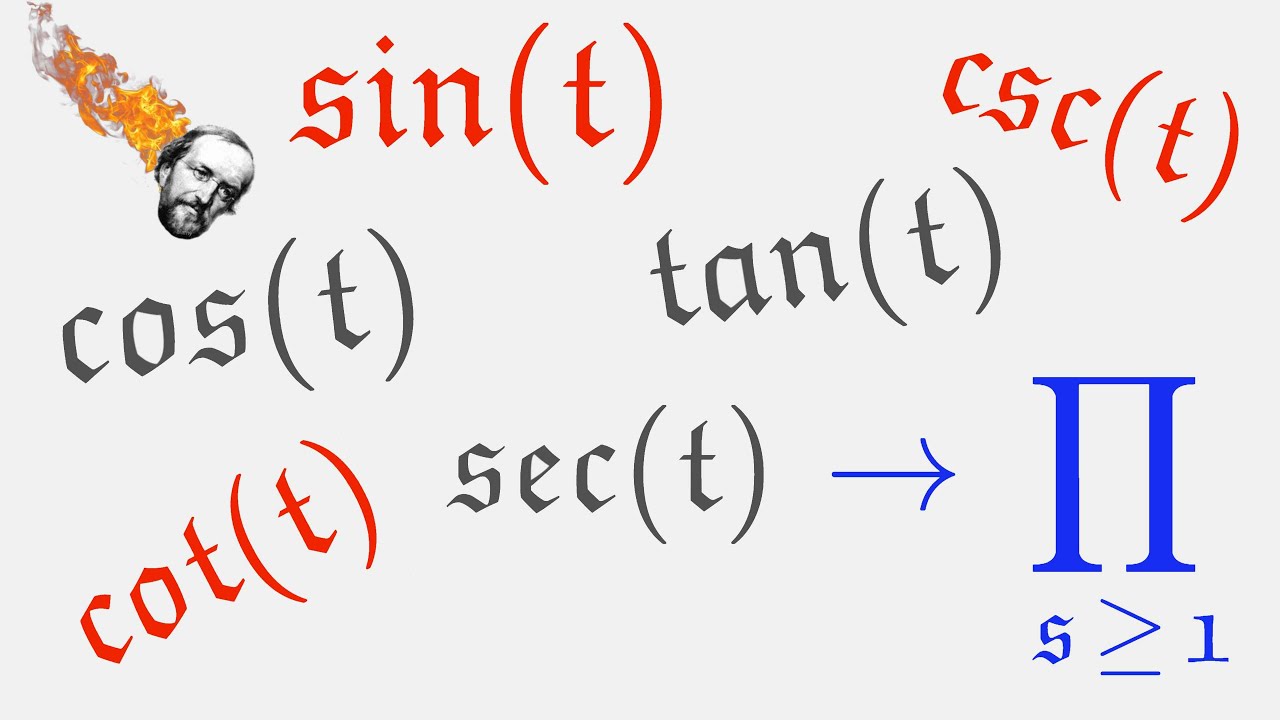
Показать описание
Help me create more free content! =)
2nd Channel:
Good morning my dear children! Let us derive a lot of cool identities today! By starting off with the Cosine, we use the double angle formula to turn it into a quotient of sin waves. From there on out we can get ourselves the tangent, cotangent, etc.! Enjoy! =D
2nd Channel:
Good morning my dear children! Let us derive a lot of cool identities today! By starting off with the Cosine, we use the double angle formula to turn it into a quotient of sin waves. From there on out we can get ourselves the tangent, cotangent, etc.! Enjoy! =D
Deriving the Infinite Product Representations for all the Trigonometric Functions!
How-to: Establish the infinite product representation of sine and cosine.
An Infinite Product for Pi
ONE NEAT PROOF! Deriving the EULER DEFINITION of the Gamma Function!
Zeta Function - Infinite Product Representation (Euler Product)
An Interesting Infinite Half-Angle Product Representation for the sin(x)
Weierstrass definition of Gamma function | infinite product representation of gamma function
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Every Student Should See This
Infinite product formula for sin(x)
Deriving EULER's INFINITE SINE PRODUCT using the Mittag-Leffler Pole Expansion of the Cotangent...
When mathematicians get bored (ep1)
Infinite Product Representation Of The Sine
Infinite Products: Example 1
That's right, an infinite product for sin(x) courtesy of Euler (feat. a crazy series for cot(x)...
How REAL Men Integrate Functions
Integrating An Infinite Product #shorts
Gamma Function: Infinite Product Definition
Ramanujan's Magnificent Formula For π #ramanujan #mathematics #maths
a great first infinite product!
(SCx36g) Infinite Products
AKPotW: Infinite Product of a Sequence [Convergence]
What's so special about Euler's number e? | Chapter 5, Essence of calculus
A Wallis type infinite product.
Комментарии
 0:15:36
0:15:36
 1:04:51
1:04:51
 0:05:54
0:05:54
 0:23:28
0:23:28
 0:13:39
0:13:39
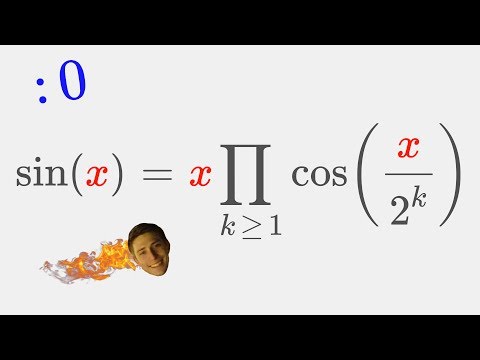 0:10:04
0:10:04
 0:06:28
0:06:28
 0:00:38
0:00:38
 0:00:58
0:00:58
 0:01:18
0:01:18
 0:11:37
0:11:37
 0:00:37
0:00:37
 0:20:20
0:20:20
 0:05:58
0:05:58
 0:15:36
0:15:36
 0:00:35
0:00:35
 0:00:58
0:00:58
 0:42:57
0:42:57
 0:00:37
0:00:37
 0:08:14
0:08:14
 0:23:00
0:23:00
 0:07:02
0:07:02
 0:13:50
0:13:50
 0:28:32
0:28:32