filmov
tv
Continuity of Multivariable Functions

Показать описание
Welcome to my video series on Multivariable Differential Calculus. You can access the full playlist here:
Videos by Zack Cramer, University of Waterloo. Textbook reference: Calculus: Early Transcendentals by Jon Rogawski, Colin Adams, and Robert Franzosa
Videos by Zack Cramer, University of Waterloo. Textbook reference: Calculus: Early Transcendentals by Jon Rogawski, Colin Adams, and Robert Franzosa
Continuity of Multivariable Functions
Calculus 3 Lecture 13.2: Limits and Continuity of Multivariable Functions (with Squeeze Th.)
Limits are...weird...for multi-variable functions | Limits along paths
🟡05 - Limit and Continuity of Functions of Two Variables
Limits of Multivariable Functions - Calculus 3
Needham Multivariable Calculus: Continuity of Multivariable Function
Limits and continuity for multivariable functions
[Multivariable Calculus] Limits and Continuity for Multivariable Functions
Continuity of Multivariate Functions
Continuity for multivariable functions
Continuity vs Partial Derivatives vs Differentiability | My Favorite Multivariable Function
Lecture 04: Continuity of multivariable functions
Continuity of Multivariable Functions
Continuity of a Function | Two Variable Function | Multivariable Calculus
Continuity Examples
Continuity of Multivariable Functions
5.3: Continuity of multivariable functions | Wellesley College Multivariable Calculus
14.2: Limits and Continuity
Continuity in Multivariable Functions
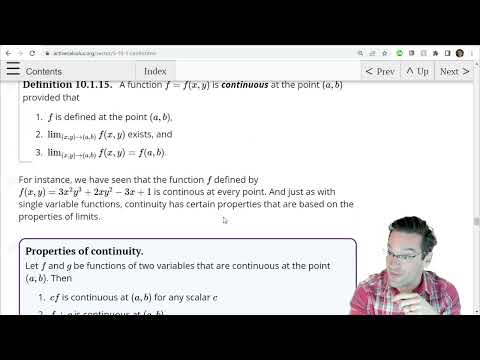
261.10.1 About Continuity of Multivariable Functions
Limits of multivariable functions
21 Continuity of Multivariable Functions
Limits and Continuity OF Multivariable Calculus
Multivariable Calculus Lecture 4 (Limits and Continuity of Functions of Several Variables)
Комментарии
 0:11:20
0:11:20
 2:14:36
2:14:36
 0:05:38
0:05:38
 0:26:31
0:26:31
 0:19:04
0:19:04
 0:06:03
0:06:03
 0:13:54
0:13:54
![[Multivariable Calculus] Limits](https://i.ytimg.com/vi/GXm0sokeVtQ/hqdefault.jpg) 0:10:20
0:10:20
 0:03:19
0:03:19
 0:29:04
0:29:04
 0:09:11
0:09:11
 0:19:25
0:19:25
 0:02:04
0:02:04
 0:13:08
0:13:08
 0:06:36
0:06:36
 0:14:55
0:14:55
 0:17:04
0:17:04
 0:34:42
0:34:42
 0:31:11
0:31:11
 0:02:37
0:02:37
 0:11:35
0:11:35
 0:10:06
0:10:06
 0:07:16
0:07:16
 0:15:11
0:15:11