filmov
tv
Discrete Math - 6.2.2 A Pigeonhole Proof

Показать описание
Your textbook does a great job of taking you through several "more elegant" applications of the Pigeonhole Principle. In this video, I take you through one that isn't showcased in your textbook in proving that 9 ordered triples must have at least one pair that have integer midpoints.
Video Chapters:
Intro 0:00
Setting up the Proof 0:31
The Proof 6:18
Up Next 11:10
Video Chapters:
Intro 0:00
Setting up the Proof 0:31
The Proof 6:18
Up Next 11:10
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
Composition of relations | MISTAKE - explained RoS instead of SoR and vice versa | otherwise correct
COMBINATIONS with REPETITION - DISCRETE MATHEMATICS
Mathematical Induction
Recurrence Relations Problem 1 - Recurrence Relation - Discrete Mathematics
Hasse Diagram with Example (Discrete Mathematics) Order relation & Lattice
The Hardest Math Test
Induction Divisibility
OUR Algebra 1 - Unit 2 Less 8 - Getting Down to Business - Mr. Morgan’s Math Help
Composition of Relation with Itself
Equivalence Relation
Discrete mathematics by Dr. Abdur Rehman | chapter 6 Permutations exercise 6.2 question 1,2,3 |
Discrete Math - 6.2.2 A Pigeonhole Proof
Equivalence Classes
Introduction to Relations
Prove by Mathematical induction that 6^(𝑛+2)+7^(2𝑛+1) is divisible by 43 for each positive integer....
Venn Diagram Problem 2 and 3 - Set Theory - Discrete Mathematics
Obtain particular solution ar + 5ar-1 + 6ar-2 = 3r2 - 2r + 1 | Jayesh Umre
Discrete Mathematics Lecture 2 | Principle of Mathematical Induction By Dr.Gajendra Purohit
Hasse Diagram
[Discrete Mathematics] Midterm 2 Solutions
What is Modular Arithmetic - Introduction to Modular Arithmetic - Cryptography - Lesson 2
Learn how to use mathematical induction to prove a formula
Hasse Diagram Problem 1 - Poset and Lattice - Discrete Mathematics
Комментарии
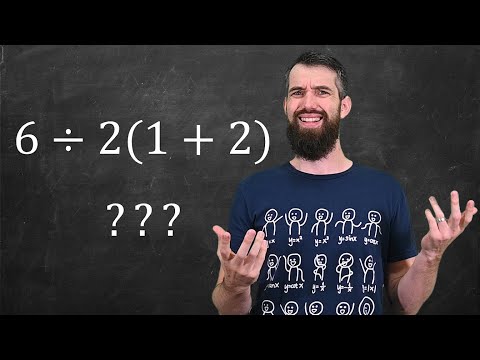 0:06:04
0:06:04
 0:03:20
0:03:20
 0:13:35
0:13:35
 0:10:04
0:10:04
 0:09:29
0:09:29
 0:02:42
0:02:42
 0:00:28
0:00:28
 0:20:35
0:20:35
 0:51:36
0:51:36
 0:06:59
0:06:59
 0:06:29
0:06:29
 0:13:21
0:13:21
 0:11:30
0:11:30
 0:07:19
0:07:19
 0:07:39
0:07:39
 0:13:53
0:13:53
 0:06:46
0:06:46
 0:10:30
0:10:30
 0:19:34
0:19:34
 0:17:08
0:17:08
![[Discrete Mathematics] Midterm](https://i.ytimg.com/vi/_8ABr2Zkfog/hqdefault.jpg) 0:33:46
0:33:46
 0:04:48
0:04:48
 0:07:08
0:07:08
 0:06:55
0:06:55